|
| Mühendishane - Makaleler | ||||||||||||||||||||||||||||||||||||
| Çarşamba, 17 Ağustos 2005 | ||||||||||||||||||||||||||||||||||||
|
Genel olarak HAD yöntemleri yaklaşık bir hesap yapar dolayısı ile analitik sonuç gibi yüksek hassasiyette çözümler oluşturamayabilirler. Yapılan analizin hassasiyeti ise öncelikle hesaplama örgüsü içindeki elemaların büyüklüklerine, konumlarına, türlerine (üçgen, dörtgen temelli) ve eleman formülasyonuna (doğrusal, 2.derece vs) bağlıdır. HAD yazılımlarının çok yüksek hesaplama zamanı gerektirebilmeleri, problemlerin modellenmesi, çözümlenmesi ve sonuçların doğru olarak değerlendirilebilmesinin zor olması ve hataya açık olması ve özellikle ilk kullanılan örneklerin yeterli sonuç hassasiyetine sahip olmaması gibi sebepler de bu teknolojinin henüz yaygın olarak kabul görememesini açıklayabilir. Burada konuyla yeni ilgilenmeye başlayanlar için giriş seviyesinde bazı bilgiler sunulmaya çalışılacaktır. Bunun yanında en azından temel akışkan dinamiği bilgisine sahip olduğunuz varsayılacaktır. Konunun nazarî temeline sahip olmadan hesaplamalı akışkan dinamiği teknolojisinden etkin olarak yararlanabilmek pek mümkün olmaz. Son birkaç sene içerisinde "düğmeye bas/sonuç al" şeklinde çalışan çok sayıda HAD yazılımı ortaya çıktı ve büyük pazar sebebiyle de bu tip tam otomatik yazılımların daha da artacağını tahmin edebiliriz. Fakat, akışkan dinamiği konusu bu kadar basit değildir. Evet artık mevcut yazılımlarla birkaç tıklamayla çok güzel renkli resimler :oP elde edilebiliyor ama sonuç gerçeğe ne kadar yakın? Açık konuşmak gerekirse bu teknolojinin bilerek veya bilmeyerek kötüye kullanılması, başarılı benzetimler yapmaktan çok daha kolay. Tabii ki bu durum HAD'ı kullanmayacağımız anlamına gelmez. Sadece daha iyi bilgi, tecrübe ve altyapıya sahip olup kendimizi yetiştirmemiz gerektiği anlamına gelir. Tamamen benzer bir durum sonlu elemanlar yöntemi ile yapılan yapısal hesaplamalar için de geçerlidir. HAD'ın zaman içinde gelişimi kabaca şu sırada gerçekleşmiştir;
Hesaplamalı akışkan dinamiği nerede kulanılır ve ne zaman tercih edilir;
HAD'ın gemi mühendisliği alanındaki başlıca uygulama alanları:
olarak sıralanabilir. Bir HAD uygulaması üç+bir temel aşamadan meydana gelir:
1.ÖNİŞLEMÖnişlem; incelenecek problemin çözüm aşamasına getirilmesi için yapılan bütün çalışmaları kapsar ve kullanılacak çözüm yöntemine uygun bir çalışmayı gerektirir. Genelde geometrik modelleme işin başlangıç noktasıdır. Herhangi bir bilgisayar destekli tasarım yazılımıyla oluşturulmuş, ihtiyaca göre 2 ya da 3 boyutlu bir geometrik model HAD sistemine ithal edilerek kullanılabileceği gibi doğrudan, kullanılan HAD yazılımının önişlemcisinde de geometri oluşturulabilir. Mevcut ticari yazılımların çoğu .iges formatında geometri ithali ve ihracı yapabilmektedir. Fakat belirtmek gerekir ki çeşitli yazılımlar arasında .iges ile geometri alış verişi yapmak sıklıkla sorunlara sebep olabilmektedir. Ayrıca bazı gelişmiş BDT yazılımlarının içinde onun uzantısı gibi çalışabilen HAD sistemler de mevcuttur. Bu durumda geometri transferinde yaşanan sorunlar ortadan kalkmış olur.
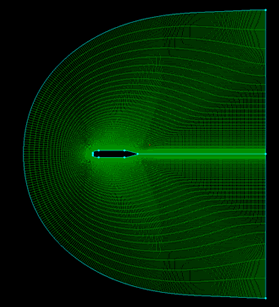
Resim.1) Bu yazıdaki örnekler için geometrisi kullanılacak olan 400mm bir tel güdümlü torpilin 1:1 3B yüzey modeli Geometrinin oluşturulmasını problemin etki alanının belirlenmesi ve bu alanda (3 boyutlu uygulamalar için bu hacimde) hesaplama örgüsünün oluşturulması takip eder. Basit olarak açıklamaya çalışırsak örgü; etki alanının çok küçük alt hesap alanlarına (veya hacimlerine) bölünmesi ve gerekli matematiksel çözümlerin tüm bu örgülerin düğüm noktalarında ayrı ayrı yapılıp elde edilen verilerin değerlendirilmesi yoluyla bütün hesaplama alanı içindeki nihai çözümün elde edilmesi için kullanılır.
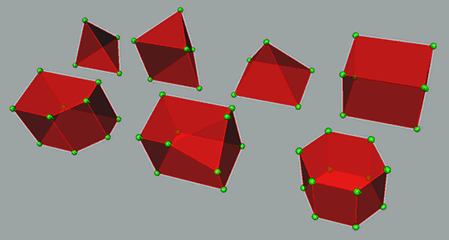
Resim.2) 2B HAD elemanları Yukarıda iki boyutlu temel örgü elemanları görülüyor. Serbest örgülerde bunların tamamı kullanılabilirken düzenli örgülerde sadece dörtgen temelli olanlar kullanılabilir. Burada kırmızı; örgü elemanlarını ve yeşil; düğümleri gösterir. Aşağıda ise üçgen, dörtgen ve çokgen temelli, 3 boyutlu çeşitli örgü elemanları görülüyor. Yeni geliştirilen bazı uygulamalarda çokgenler (alt sıra) kullanan örgü yöntemleri de kullanılmaya başlanmıştır.
Resim.3) 3B HAD Elemanları Hesaplama alanı içindeki örgü yoğunluğu ne kadar fazla olursa genel olarak akışkan dinamiği çözümünün hassasiyeti artar diyebiliriz (fakat bu kabûl her zaman geçerli olmayabilir) Diğer taraftan bu durum yapılacak hesaplamanın toplam süresini de oldukça arttırır ve hatta hesaplamayı, eldeki bilgisayar sisteminin imkânları dahilinde, imkânsız hale getirebilir. Bugün için bir akışkan dinamiği çalışmasının en zor, zaman alan ve tecrübe gerektiren bölümünü önişlem oluşturur denilebilir çünkü oluşturulan hesaplama örgüsünün nitelikleri çözücünün performansını doğrudan etkilediği gibi sonuçların doğruluğunu ve hassasiyeti büyük ölçüde belirler. Yaygın olarak kabul görmüş iki farklı temel önişlem yöntemi mevcuttur:
Düzenli örgü yöntemleri eliptik, hiperbolik ve cebirsel olarak adlandırılan çeşitli hesaplama teknikleri kullanırlar. Günümüzde düzenli örgü oluşturma algoritmaları karmaşık geometriler etrafında da başarıyla örgü oluşturabilecek kadar gelişmiştir. Bununla birlikte bazı karmaşık 3 boyutlu geometriler söz konusu olduğunda bu işlem genellikle çok zaman alıcı olmaktadır.
Resim.4) 400m torpil gövdesi için oluşturulmuş 2B düzenli örgü Düzenli örgü, basit geometriler için, serbest örgüye göre daha az hesaplama hücresi kulanarak daha yüksek kalitede çözümler üretebilir. Karmaşık 3 boyutlu geometriler söz konusu olduğunda ise düzenli örgü oluşturmak çok zorlaşır ve oluşturulabilse bile sonuçta yukarıdaki üstünlüklerini kaybedebilir. Düzenli örgüler adından da anlaşılacağı gibi elemanlar arasındaki muntazam bağlantılarla tanımlanırlar. Düzenli örgüyü oluşturan elemanlar özgün olarak tamamen dörtgen temellidir. 2B için her düğüm noktası dört elemanı bağlar.
Resim.5) Yukarıdaki düzenli örgünün torpil burnundaki yakın görünüşü. Karmaşık geometriler etrafında kolayca örgü oluşturabilme ve bunların etrafındaki akışı otomatik olarak hesaplayabilme arzusunun bir sonucu olarak serbest örgüler geliştirilmiştir. Serbest örgü karmaşık geometrilerin işlenmesi ve örgünün akış şartlarına uyarlanması konularında önemli esneklik sağlar. Serbest örgü genelde üçgen temelli elemanlardan (dörtgen ve çokgen elemanlar da içerebilir) meydana gelir. Serbest örgü kullanarak hesaplama örgüsü oluşturmak çok az kullanıcı girdisiyle neredeyse tam otomatik hale getirilebilir ve karmaşık geometriler etrafında kolaylıkla oluşturulabilir. Serbest örgüler herhangi bir düğümde herhangi bir miktarda elemanın bağlanmasına izin verirler. Temelde otomatik örgü oluşturma yöntemlerinde kullanılmak üzere geliştirilmişlerdir. Serbest örgü teknikleri karmaşık geometrilere kolayca uyar ve elemanların fazla çarpılmasına engel olacak şekilde eleman büyüklüğünü değiştirebilir bu nedenle akışkan dinamiği uygulamalarında başarıyla kullanılabilir. Son birkaç yılda oldukça yaygınlaşmaya başlayan ve otomasyona yatkınlığı ve kolaylığıyla öne çıkan bir yöntem olan serbest örgü izafi olarak daha kolay bir öğrenme ve modelleme süreci sağlayabilmesi sayesinde önümüzdeki yılların temel yöntemi olacak gibi gözükmektedir. Bu nedenle pek çok önde gelen ticari HAD yazılımları eski sürümlerinde sadece düzenli örgü ile çalışabilirken artık serbest örgüyü desteklemeye başlamışlardır. Bununla birlikte düzenli örgünün üstünlükleri de mevcuttur. Her iki yöntemi bir arada kullanan melez örgüler özellikle bazı problemlerde en uygun tercih olarak kullanılabilirler.
Resim.6) Aynı modelin bu defa "serbest örgü" ile hazırlanmış burun ayrıntısı. Yukarıda kısaca değinilen iki temel örgü oluşturma yönteminden başka kartezyen örgü yöntemlerini ayrıca ele almak yerinde olur. Kartezyen örgü yöntemlerinin geliştirilmeye başlanması 1970'lere kadar gider. Dikkât çekmeye başlamaları ise "uyarlanmış örgü iyileştirme" uygulamasının yönteme eklenmesiyle gerçekleşmiştir. Bu uygulamanın geliştirilmesi ise ancak son 10 yıl içinde olmuştur.
Resim.7) 400mm torpil modeli üzerinde oluşturulmuş 3B kartezyen örgü Yukarıda, Resim.7'de görülen torpilin kıçındaki bu karmaşık geometri sebebiyle tüm torpil gövdesi üzerinde 3 boyutlu bir düzenli örgü oluşturmak oldukça zordur ve tahminen (kullanıcının tecrübesine ve kullanılan yazılımın niteliklerine de bağlı olarak) 60-120 saatlik bir emek gerektirebilir. Bu yapı üzerinde serbest örgü oluşturmak da pek kolay sayılmaz, tahminen 5-10 saat zaman alabilir. Oysa bu kartezyen örgüyü oluşturmak geometrinin ithâlinden itibaren yaklaşık 3 dakika sürdü. Bir HAD hesaplamasında temel incelik problemi çözmek için gereken doğrulukta bir örgü oluşturmaktır. Eğer örgü çok kabaysa (düşük çözünürlük) doğru çözüm elde edilemeyebilecektir. Eğer çok inceyse (yüksek çözünürlük) bu defa problemin çözüm süresi kabul edilemeyecek seviyelere çıkabilecektir. Bunun yanında kullanılan çözüm yöntemleri ve türbülans modellerinin gerektirdiği doğru örgü büyüklüklerini de sağlayabilmek gerekebilir. İyi veya uygun bir örgü, altta yatan fiziksel olayların etkin olarak hesaplanabilmesine olanak sağlarken hızlı bir çözüm elde etmek için yeteri kadar da kaba olmalıdır. Genel olarak doğrusal elemanlar parabolik olanlardan, parabolikler de kübiklerden daha ince bir örgü gerektirirler. Uygun bir örgü tanımlayabilmek için hesaplama alanı içinde değişkenlerin (basınç, sürât, sıcaklık gibi) dağılımının bilinmesi gereklidir. Eğer bilinirse o zaman iyi bir örgü tanımlanabilir. Değişkenlerin ani ve belirgin olarak değiştiği hesaplama alanı bölgelerinde daha ince örgü ve önemli değişiklikler göstermediği hesaplama alanı bölgelerinde de daha kaba örgü kullanılarak başarılı bir örgü oluşturulabilir. Uyarlanabilir örgü iyileştirme yöntemleri bu noktada büyük faydalar sağlayarak çözüm esnasında hesaplama alanında oluşan değişken değerlerini temel alıp örgü üzerinde, sadece ihtiyaç duyulan bölgeler için iyileştirme yaparak nihaî sonucun hassasiyetini artırabilirler. Kullanılan yazılıma bağlı olarak düzenli, serbest ve kartezyen örgü yöntemleri için çeşitli uyarlanmış örgü iyileştirme teknikleri mevcuttur. Bu nedenlerle herhangi bir HAD kullanıcısı altta yatan fiziksel olaylar hakkında temel bilgiye sahip olmalıdır. Hesaplama alanındaki her bir örgü elemanı, temel ana elemanın şekline göre tanımlanır. Hesaplama alanının geometrisi sebebiyle örgüyü oluşturan elemanların özellikle geometrik model sınırlarıyla temas eden bölgelerde şekli geometriye uymak için değişir ve temel eleman şekline göre bir miktar çarpılır. Bu çarpılma elemanın etkinliğini bir miktar azaltır ve çarpılma arttıkça çözüm hataları gitgide büyür. Bu nedenle kullanıcı hesaplama örgüsünü oluştururken mümkün olduğu kadar elemanların çarpılmalarını azaltmaya ve temel eleman şeklini korumaya çalışmalıdır. 2. bölümde HAD çözüm yöntemleri genel hatlarıyla ele alınacaktır!
Tablo.1) Konuyla ilgili bazı İngilizce terimler için kullanılan Türkçe karşılıklar Yaftalar: ♦ Kaynaklar1. Introduction to Computational Fluid Dynamics, Tao Xing, Fred Stern2. Naval Hydrodynamics Benefits from Using CFD, Gridgen 3. Review of CFD, ME 681 CFD class notes 4. Trends in CFD, Engineering Analysis&Computing, An Introduction to CFD for Incompressible Flow, Mark A. Christon 5. An adaptive Cartesian grid generation method for "Dirty" geometry Z. J. Wang1 Kumar Srinivasan 6. Adaptive Cartesian Mesh Generation M. J. Aftosmis M. J. Berger J. E. Melton 7. The hitchhikers guide to CFD, K.Jones |