|
 Önceki bölümde Takviyesiz İnce Cidarlı Konik Kabuklar sonlu elemanlar yöntemi yaklaşımı ile kısaca ele alındıktan sonra denizaltı mukavim tekneleri üzerinde de yaygın olarak kullanılmasıyla önemli bir yapısal alt başlık olan kemerelerle desteklenmiş takviyeli koni konusuna sıra geldi. Önceki bölümde Takviyesiz İnce Cidarlı Konik Kabuklar sonlu elemanlar yöntemi yaklaşımı ile kısaca ele alındıktan sonra denizaltı mukavim tekneleri üzerinde de yaygın olarak kullanılmasıyla önemli bir yapısal alt başlık olan kemerelerle desteklenmiş takviyeli koni konusuna sıra geldi.
Bu tür bir çalışmada denel doğrulama faaliyeti son derece önemli olduğu için konuya yine bu doğrultuda bir giriş yapmak uygun olacaktı ve kolayca ulaşılabileceği için [1] üzerinde yayınlanan deney ve hesaplama çalışmalarının temel alınması tercih edildi.
Üç farklı ölçüdeki kemere ile desteklenmiş eşdeğer simetrik metal konilerin harici hidrostatik yük altındaki plastik burkulmasının incelendiği söz konusu makalede yayınlanan denel ölçüm verileri ve hesaplama sonuçları ile bir karşılaştırma yapabilmek için öncelikle açık-kaynak Gmsh [2] yazılımı kullanılarak önişlem safhası gerçekleştirildi.
Bu tür bir yapıyı farklı şekillerde modellemek düşünülebilirdi, burada hem koni hem de kemereler için 2B cidar elemanları kullanılmak yönünde bir tercih yapıldı. Hesaplamaları için ise Calculix ccx kullanıldı. Aslına bakılırsa Calculix [3] gerek kiriş gerekse kabuk elemanları için de katı elemanlar kullanmakta, bir ve iki boyutlu elemanları da hesaplamadan önce üç boyutlu hâle dönüştürmektedir.
♦ gmsh: // Takviyeli İnce Cidarlı Koni Burkulma Doğrulama Çalışması İçin // Kaynak: Plastic buckling of ring-stiffened conical shells // under external hydrostatic pressure, 2004 // Carl T.F. Ross - Andrew P.F. Little - Kehinde A. Adeniyi // Akma Mukavemeti= 250MPa / Esneklik Katsayısı= 193e09Pa / Poisson Oranı= 0,3 // Üsküdar Mühendishanesi - http://uskudar.biz // Konilerin Tanımlalanmaları // Koni10 A = 0.0025; B = 0.0015; t = 0.0020; // Koni11 //A = 0.0025; //B = 0.0020; //t = 0.0020; // Koni12 //A = 0.0025; //B = 0.0025; //t = 0.0020; // Temel Ölçüler r1 = 0.101675/2; // büyük yarıçap, m r2 = 0.060000/2; // küçük yarıçapı, m x0 = 0.116500; // uzunluk, m x1 = 0.013250; // kısa aralık x2 = 0.022500; // uzun aralık Geometry.CopyMeshingMethod = 1; Point(0) = {0, 0, 0}; // merkez Point(10) = {0, r2+t, 0}; Point(11) = {0.01325,0.032369930+t,0}; Point(12) = {0.03575,0.036394340+t,0}; Point(13) = {0.05825,0.040418750+t,0}; Point(14) = {0.08075,0.044443160+t,0}; Point(15) = {0.10325,0.048467570+t,0}; Point(16) = {0.11650,r1+t,0}; Point(21) = {0.01325,0.032369930+B+t,0}; Point(22) = {0.03575,0.036394340+B+t,0}; Point(23) = {0.05825,0.040418750+B+t,0}; Point(24) = {0.08075,0.044443160+B+t,0}; Point(25) = {0.10325,0.048467570+B+t,0}; Line (30) = {10,11}; Line (31) = {11,12}; Line (32) = {12,13}; Line (33) = {13,14}; Line (34) = {14,15}; Line (35) = {15,16}; Line (41) = {11,21}; Line (42) = {12,22}; Line (43) = {13,23}; Line (44) = {14,24}; Line (45) = {15,25}; Transfinite Line {30,35} = 5; Transfinite Line {31,32,33,34} = 8; Transfinite Line {41,42,43,44,45} = 3; d1 = 24; // Çeyrek için düğüm sayısı Extrude { {1,0,0} , {0,0,0} , -Pi/2} { Line{30,31,32,33,34,35,41,42,43,44,45}; Layers{d1}; Recombine; } Extrude { {1,0,0} , {0,0,0} , -Pi/2} { Line{46,50,54,58,62,66,70,74,78,82,86}; Layers{d1}; Recombine; } Extrude { {1,0,0} , {0,0,0} , -Pi/2} { Line{90,94,98,102,106,110,114,118,122,126,130}; Layers{d1}; Recombine; } Extrude { {1,0,0} , {0,0,0} , -Pi/2} { Line{134,138,142,146,150,154,158,162,166,170,174}; Layers{d1}; Recombine; } // CalculiX için gerekli bâzı ayarlar Mesh.SecondOrderIncomplete=1; // 2.derece elemanları doğru ihrac etmek için gerekli Mesh.SaveGroupsOfNodes = 1; // düğüm gruplarının kaydedilmesi için Mesh.ElementOrder = 2; // ikinci derece elemanlar için 2 // CalculiX için adlandırmalar Physical Line("mesnetk") = {47,135,179,91}; Physical Line("mesnetb") = {112,200,156,68}; Physical Surface("cidar") = {93,97,101,105,109,113,181,185,189,193,197,201,137,141,145,149,153,157,49,53,57,61,65,69}; Physical Surface("kemere") = {205,209,213,217,221,161,165,169,173,177,73,77,81,85,89,117,121,125,129,133};
Velhâsıl yukarıdaki Gmsh betiği ile [1]'de tanımlanan üç adet koni geometrisi (10, 11 ve 12) için gereken hesaplama örgüsü kolayca oluşturulabilir ve istenilen çözücüye uygun olarak ihraç edilebilir ki burada çözücü CCX olacağı için hazırlık da buna uygun olarak yapılmış ve S8 türü elamanlara elde edebilmek amacıyla düzenli örgü meydana getirilmiştir.
Bu safhada yukarıdaki önişlem verileri kullanılarak, sadece doğrusal burkulma yaklaşımı ile elde edilen sonuçların [1] üzerinde verilen deney ve hesaplama sonuçları ile karşılaştırılması aşağıdaki çizelgede görülebilir.
| MPa |
Yaklaşım |
Koni 10 |
Koni 11 |
Koni 12 |
| CCX |
Doğrusal |
63,30 |
73,55 |
84,48 |
| Ansys |
Doğrusal |
62,35 |
74,22 |
83,15 |
| Pc |
Deney |
14,30 |
15,80 |
18,80 |
Çizelge.1) Calculix (2.13) ile hesaplanan, hidrostatik basınç altındaki burkulma yüklerinin (MPa) [1]'de beyan edilen ticarî Ansys yazılımı ve Deney sonuçlarıyla karşılaştırılması.
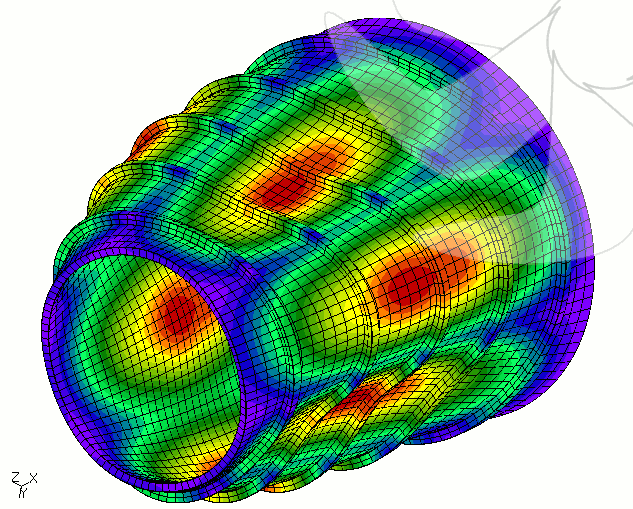
Resim.1) Takviyeli Koni 12 için CCX ile hesaplanan, hidrostatik yük altındaki ilk doğrusal burkulma modu.
Takip edecek bölümde hem takviyeli hem de takviyesiz konik kabukların, eldeki mevcut deney sonuçları ile birlikte doğrusal-olmayan burkulma davranışları ele alınmaya çalışılacak...
♦ Kaynaklar1. Plastic Buckling of Ring-Stiffened Conical Shells Under External Hydrostatic Pressure, 2004, Carl T.F. Ross - Andrew P.F. Little - Kehinde A. Adeniyi
2. Gmsh genelağ sitesi- http://gmsh.info
3. Calculix genelağ sitesi - http://calculix.de
|

