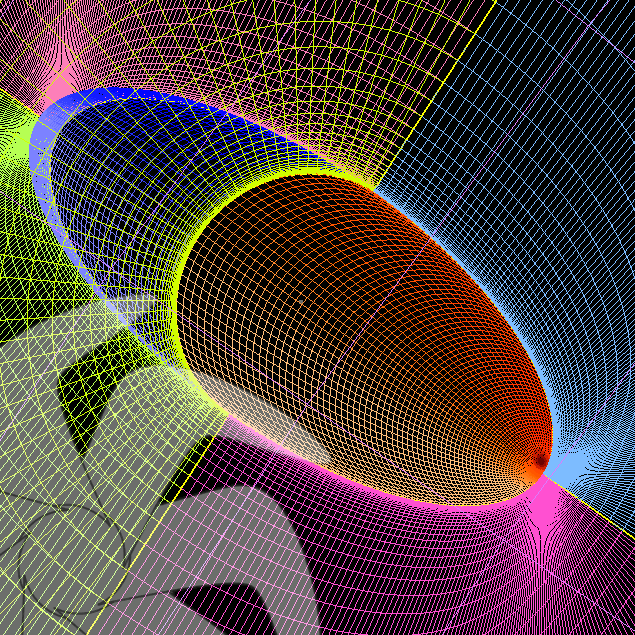Bilâhare ele alınması düşünülen 1:1 ölçekli torpil gövdeleri etrafındaki üç boyutlu akışın sayısal olarak incelenmesi mevzusunda eldeki imkânlarla kullanılabilecek en uygun benzetim yaklaşımlarının tespit edilebilmesi için her zamanki gibi öncelikle bazı doğrulama çalışmalarına ihtiyaç vardı.

Söz konusu çalışmalardan ilk safhasında kendisi basit ama etrafında oluşan akış son derece karmaşık olan 6:1 oranlarında uzatılmış küre olarak tanımlanan cisim kullanılacaktır. Bu cisim akışkan dinamiği camiası tarafından hem deney hem de sayısal çözümler için yaygın olarak tercih edilmektedir ve elde geniş bir akademik bilgi birikimi mevcuttur.

Problemin tanımlanması, çözülmesi ve değerlendirilmesi için Üsküdar Mühendishanesi tarafından sıklıkla tercih edilen dört mükemmel açık kaynaklı yazılım kullanılacaktır:

1. Gmsh; önişlemci
2. OpenFOAM; çözücü
3. ParaView; sonişlemci
4. Gnumeric; hesap çizelgesi

Özellikle denizaltı, torpil, füze gibi cisimlerin akışkan mekaniği açısından incelenmesi amacıyla çeşitli oranlarda (çoğunlukla 6:1 ve 3:1) uzatılmış küre ya da başka bir ifadeyle elipsoit geometrileri hem rüzgâr tünellerinde tecrübî olarak hem de yazılım vasıtasıyla hesaplamalı olarak uzun senelerdir incelenmektedir.

Bu sayfaya konu olan çalışma için de 6:1 oranında 2,4m uzunluğunda bir elipsoit kullanılacaktır. Gerçekleştirilecek inceleme türü için yarım elipsoit geometrisi yeterli olacağından uzun hesaplama sürelerini kısaltabilmek amacıyla 3B çözüm ağı eksensimetrik olarak sadece 0-180derece aralığında oluşturulmuştur.

Resim.1) Gmsh kullanılarak yarım elipsoid geometrisi üzerine inşa edilen düzenli hesaplama örgüsünün cisim civarındaki görünüşü.

İnşa edilen 3B çözüm ağı 540.000 hücreden (535.500 altıyüzlü + 4.500 prizma) müteşekkildir. Ağ, bu safhada sadece yüksek-Re türbülans modelleri ile çalışılacağından, başlangıç nazarî yArtı değeri 50 civarında olacak şekilde oluşturulmuştur. Bununla birlikte benzetimler sonucunda bütün türbülans modelleri üzerinden ulaşılan ortalama yArtı değeri 17,55 - azami yArtı değeri de 34,74 olarak gerçekleşmiştir.

Aslında duvar fonksiyonları kullanırken yArtı değerinin daima 30'dan büyük olması uygun olurdu. Bu durum çözümler üzerinde olumsuz bir etki yapacaktır. Kaldı ki direnç vesaire gibi cisim üzerinde oluşan kuvvetlerin hesaplanması söz konusuysa duvar fonksiyonlarının kullanılmasından tamamen kaçınmak daha uygun olarak kabûl edilebilir. Diğer taraftan 6:1 elipsoit üzerinde yapılan deney çalışmalarının yapı üzerinde oluşan kuvvetlerin ölçülmesinden ziyade çok daha karmaşık meseleler olan geçiş bölgesinin tespiti ve akış ayrılması açısından gerçekleştirildiğini belirtmek gerekir.

Yine de burada yapılan benzetim çalışmaları sadece başlangıç olduğundan, yArtı için elde edilen bu olumsuz değerlerin ve duvar fonksiyonlarının sonuç üzerinde ne derecede etkili olabileceğini anlayabilmek için bu ilk değerlendirmede elde edilen veriler sonraki çalışmalarla karşılaştırılarak önemli bir fayda sağlanabilir.

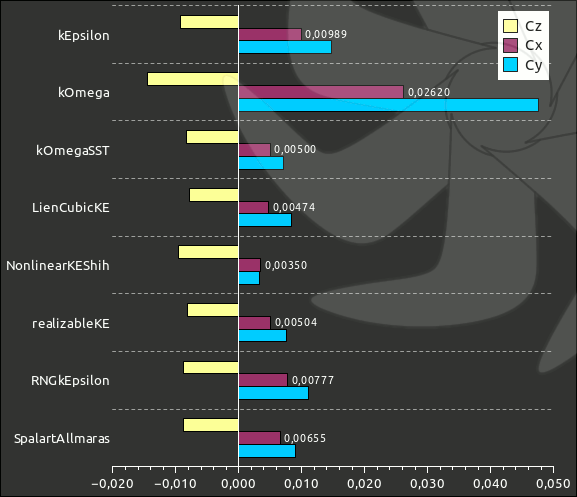
Resim.2) Kullanılan ilk sekiz yüksek-Re türbülans modelinin 2.000 tekerrür sonunda elde edebildiği direnç, kaldırma ve moment katsayıları. kOmega ile elde edilen değerlerdeki büyük sapma muhtemelen bu modelin, giriş sınır şartlarına karşı çok hassas olmasından kaynaklanmış olabilir.

İlk değerlendirme için OpenFOAM tarafından yüksek-Re örgüler için sağlanan türbülans modellerinden:

1. kEpsilon
2. kOmega
3. kOmegaSST
4. LienCubicKE
5. NonlinearKEShih
6. realizableKE
7. RNGkEpsilon
8. SpalartAllmaras

kullanılmıştır. Diğer taraftan şimdilik kararlı bir çözüm elde edilemeyen diğer birkaç yüksek-Re türbülans modelinin daha sonra ayrıca ele alınması da düşünülebilir. Alçak-Re türbülans modelleri ile DES ve LES modelleri de sonraki safhalarda incelenmeye çalışılabilir.

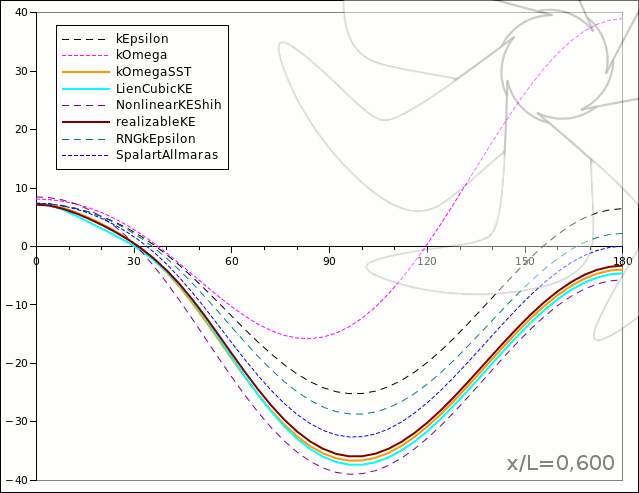
Resim.3) x/L=0,600 kesiti üzerinde oluşan basınç dağılımlarının türbülans modellerine göre davranışı.

Çözümler bu safhada sadece durağan hâl¹ için inceleneceğinden SIMPLE² algoritması kullanılmıştır. Re=4,2e06 ve HA³=10derece için elde edilen sonuçların çok kısa bir değerlendirmesi sayfadaki muhtelif resimlerde görülebilir.

Bütün modeller için benzetimler 2.000 tekerrür boyunca sürdürülmüştür. Tek işlemci ile hesaplama süreleri en hızlı; 176dk (SpalartAllmaras) ve en yavaş; 234dk (LienCubicKE) olarak gerçekleşmiştir. Kullanılan OpenFOAM sürümü 2.3.1 olup 64bit Linux işletim sistemi üzerinde çalıştırılmıştır, işlemci ise AMD Phenom II X6 1055T'dir.

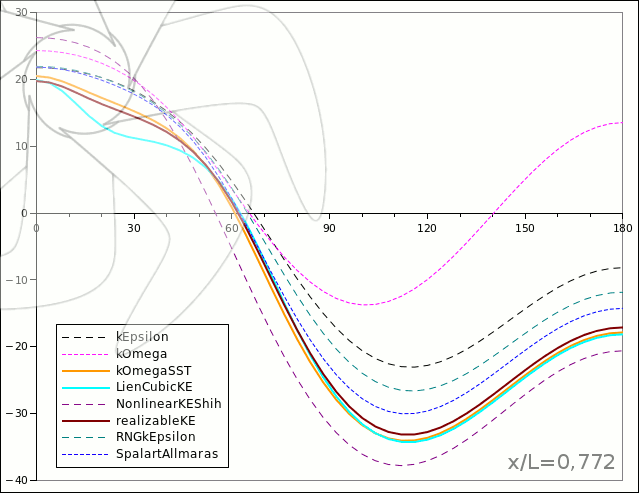
Resim.4) x/L=0,772 kesiti üzerinde oluşan basınç dağılımlarının türbülans modellerine göre davranışı.

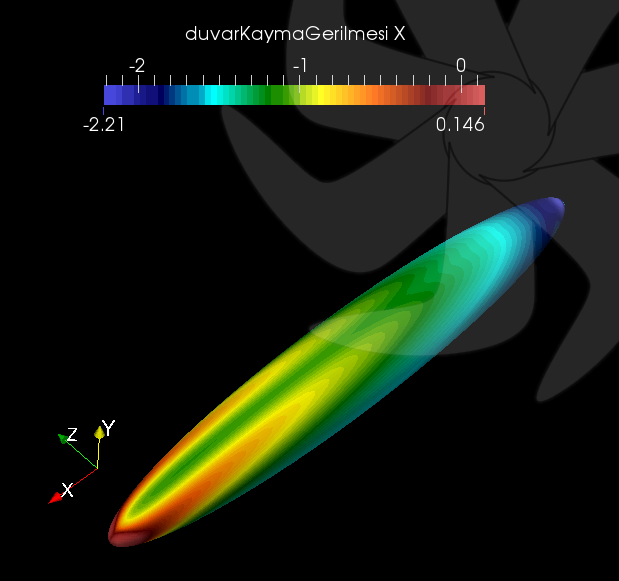
Resim.5) kOmegaSST modeli için cismin rüzgaraltı yüzeyinde hesaplanan duvar kayma gerilmesinin x bileşeni. Bu türbülans modeli, akış ayrılmasını, kullanılan diğer RANS⁴ modellerine göre daha doğru olarak tespit edebilme yeteneğine sahip olarak kabûl edilmektedir.

Şimdilik kOmegaSST ve realizableKE modellerinin bu tür bir problem için diğerlerinden daha iyi bir davranış sergilediği söylenebilir. LienCubicKE modeli de incelenmeye değer olarak kabul edilebilir. Şimdilik deney sonuçları ile doğrudan bir karşılaştırmaya gidilmedi, ancak HA=20derece ve 30derece için çözümler de elde edildikten sonra deney sonuçlarıyla karşılaştırma yapılması düşünülüyor. Yüksek-Re modelleri açısından bakılırsa sonraki hücum açıları için, burada denenen ilk sekiz türbülans modelinden dördü bu çalışma sonuçlarına bağlı olarak elendi, kalanlar; kOmegaSST, realizableKE, LienCubicKE ve bazı açılardan pek iyi bir performans göstermese de SpalartAllmaras. İkinci safhada bu dört model 20 ve 30 derecelik hücum açısında yine Re=4,2e06 için denenecek...

A summary of this page is available in English