Herhangi bir cisim ve pek çok madde uyartıldığında titreşir ki bu uyartımlar muhtelif şekillerde gerçekleşebilir; mesela bir şişenin ağzına belli hızlarda üflenmek suretiyle içindeki havanın belirgin, işitilebilir frekanslarda titreşmeye başlamasında, bir çalgının teline vurulmasında ya da bir kayığın dövünmesi esnasında bütün gövde yapısının gösterdiği tepkide gözlemlenebildiği gibi.

Nesneler sahip oldukları fiziki niteliklere bağlı olarak kendilerine has bazı frekanslarda titreşmeye eğilimlidirler ki bunlara Doğal Frekans adı verilir. Mühendislik yapılarının dinamik davranışlarının incelenebilmesi çalışmasının önemli bir parçasını da aşikâr olarak, doğal frekans hesaplamaları oluşturur. Bu amaçla sonlu elemanlar yöntemi temelli yaklaşımlar kullanmak günümüzde son derece yaygındır.

Konunun bu ilk bölümünde, gelecekteki bazı çalışmalara hazırlık maksadıyla bir takım veriler sunulacaktır. Yakın zamana kadar, cisimlerin doğal frekanslarının tespit edilebilmesine yönelik olarak analitik yaklaşımlar ve deneyler kullanılmaktaydı.

Bununla birlikte karmaşık nesnelerin doğal frekanslarını elle hesaplayabilmek pek mümkün olmadığı için özellikle hassas projelerde pahalı ve zaman alıcı denel çalışmalar yapmak gerekliydi. Artık yaygınlaşan ve ucuzlayan bilgisayar donanımı imkânlarıyla birlikte bu sahadaki ihtiyaç büyük ölçüde sayısal yöntemlerle karşılanmaya başlandı fakat yine de nazarî ve denel çalışmalara ihtiyaç kalmadığını düşünmek de son derece hatalı olur.

Yazı iki alt bölümden meydana gelecek, önce analitik çözüm yaklaşımı ve sonra tercih edilen bir yazılım vasıtasıyla yapılacak hesaplamalar ve sonuçların karşılaştırılması. Tabii, konunun nazarî tarafı burada kapsam dışı bırakılacaktır.

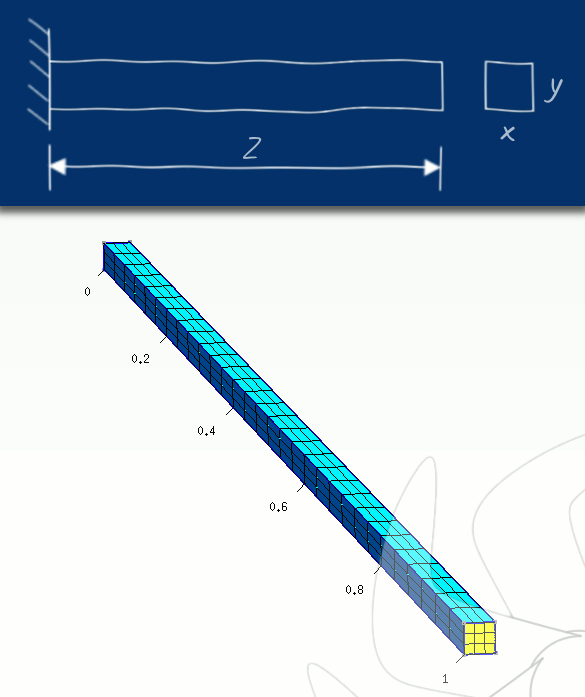
Resim.1) Çalışmada kullanılan sabit-serbest kiriş modeli. Aşağıda görülen G [Çizelge.1] örgüsü ile.

Analitik bir çözümün elde edilebilmesi ancak kolay bir şekle sahip cisimler üzerinde mümkün olabileceği için çalışmada bir ucu sabit mesnete bağlı diğer ucu serbest, kare kesitli bir kiriş tercih edilmiştir. Model olarak kullanılacak yapının [Resim.1] ihtiyaç duyulan temel nitelikleri şöyledir:

• z = 1,0 m (Uzunluk)
• x = 0,01 m (Genişlik)
• y = 0,01 m (Yükseklik)
• E = 2,07e11 N/m² (Esneklik Katsayısı)
• ro = 7.830 kg/m³ (Yoğunluk)
• nu = 0,30 (Poisson Oranı)

Yukarıdaki verileri kullanarak söz konusu sabit-serbest kirişin titreşim modları ve mod şekilleri elle hesaplanabilir. Bu amaçla aşağıdaki denklemler kullanılabilir ki bu yöntemle elde edilen ilk beş doğal frekans değeri [Çizelge.2]'de görülebilir. İlk denklemde A kesit alanı ve L uzunluktur.

1.Doğal Frekanslar için:

2.Mod Şekilleri için:

Çizelge.1) Hesaplamalar üzerinde örgü çözünürlüğünün etkisinin anlayabilmek için kullanılan muhtelif örgüler hakkındaki temel veriler. Bütün örgüler için ikinci derece p eleman kullanılmıştır. Ortalama hata verileri ilk beş mod için elde edilen hesaplama sonuçlarına ait hata mutlak değerlerinin ortalaması alınmak suretiyle elde edilmiştir.

İkinci yaklaşım olarak kullanılacak olan bilgisayar destekli yöntem için Elmer [1] adlı açık kaynaklı bir çoklu-fizik yazılımı tercih edilmiştir. Elmer Finlandiya kökenli bir çalışmanın ürünü olup 1971 yılında kurulmuş bulunan CSC [2] adlı kurum tarafından 1995 senesinde geliştirilmesine başlanmış ve 2005'den itibaren de açık-kaynak olarak yayınlanmış çok yetenekli bir yazılımdır.

Sonlu Elemanlar Yöntemi yaklaşımını kullanan Elmer; akışkan dinamiği, yapısal mekanik, elektromanyetik, ısı transferi, akustik gibi fizikî modelleri bünyesinde barındırmakta ve bunları aynı ayda ve birlikte kullanabilmeye imkân sağlamaktadır.

Böyle bir problemi farklı sonlu eleman türleriyle ele almak mümkündür; kiriş, kabuk, levha veya katı gibi. Burada kullanılacak eleman ise altıyüzlü katı olacaktır. [Çizelge.1] üzerinde hesaplamalarda kullanılan 12 farklı örgü ile alâkalı temel bazı veriler görülebilir.

Çizelge.2) Kullanılan farklı örgülerle elde edilen değerlerle analitik çözümün karşılaştırılması.

Hesaplamalar için kullanılan yazılımlar şöyledir:

• Önişlemci: Gmsh 3.0.5
• Hesaplayıcı: ElmerSolver 8.3
  • Çözücüler: StressSolve - Direct/BiCGStab | SaveScalars
• Sonişlemciler: Paraview 5.0.1 | Gnumeric 1.12.28

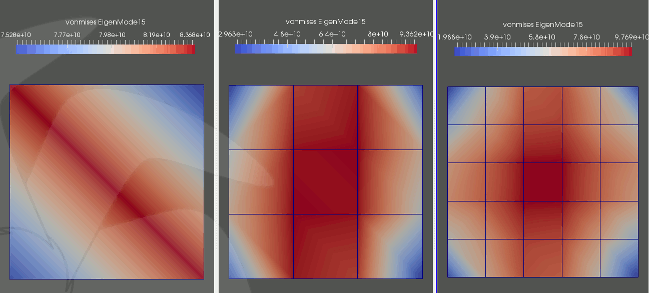
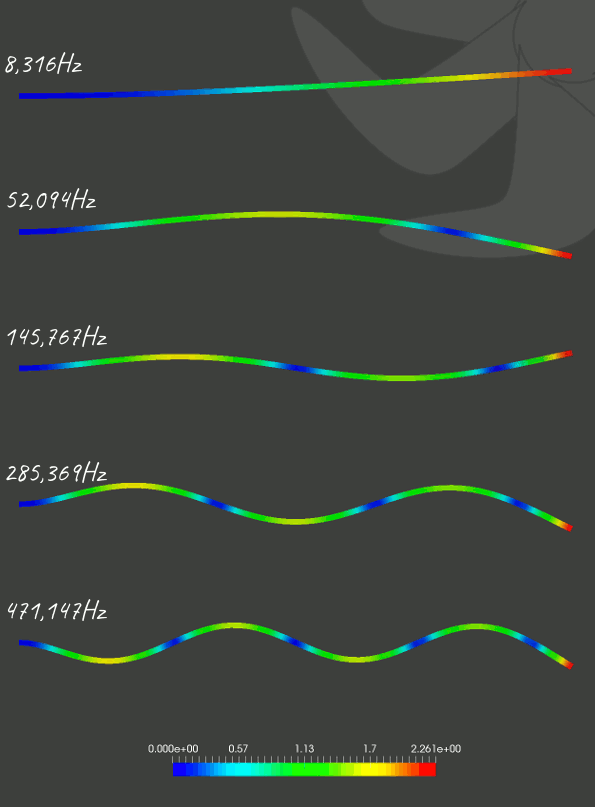
Hem elle hesaplanan hem de A'dan J'ye kadar 12 farklı örgü ile çözülen ve ilk beş titreşim modu için sunulan sonuçlar [Çizelge.2] üzerinde görülebilir.

Hesaplama süresi - hata oranı - kesit üzerindeki çözünürlük açıları [Çizelge.1] ve [Resim.2] birlikte değerlendirildiğinde "G" örgüsünün en başarılı sonucu verdiği söylenebilir.

Resim.2) H örgüsü ile üç farklı çözünürlükte için elde edilen, 15.titreşim moduna ait z/2'deki kesit üzerinde von Mises gerilmeleri. Bu gerilmelerin fizikî bir değeri olmasa da kesitteki örgü çözünürlüğünün dağılım üzerindeki etkisini göstermek için buraya eklendi...

Resim.3) Kullanılan sonlu elemanlar hesaplama yöntemiyle, H örgüsü kullanılarak ilk beş mod için elde edilen titreşim frekansları, şekilleri ve yer değiştirme değerleri.

Tabii bu çalışmada Elmer'in tercih edilmesinin bazı önemli sebepleri de var ki bunların başında sahip olduğu kapsamlı çoklu-fizik yeteneği gelmektedir. Bizim işimiz suyla olduğuna göre boşluktaki/havadaki titreşimi kolayca hesaplamak hedefimiz değil, önemli olan suyun içinde ne olacağı, öyle değil mi?

Fakat oraya gelmeden önce birkaç mevzunun daha çözülmesi gerekli...