İnce cidarlı konik kabuklar mühendisliğin bâzı alanlarında sıklıkla kullanılır ki denizcilik ve havacılık bu uygulama sahalarından en önde gelenleridir. Bu tür bir yapının tasarımında dikkât edilmesi gereken öncelikli husus, yük altındaki kabuğun yapısal kararlığını sürdürebilme yeteneğini doğru olarak tespit edebilmektir.

Burada sadece denizcilik uygulamalarına ve bu alan içinden de temel olarak sualtı uygulamalarına odaklanılacağı için muhtelif yükleme seçenekleri arasından ağırlıklı olarak hidrostatik basınç altındaki davranışları ele alınacaktır. Konik yapılar hakkındaki kısa değerlendirme toplam üç safhadan meydana gelecektir:

Bu ilk bölümde ince cidarlı takviyesiz konik kabuklar, ikinci bölümde ince cidarlı takviyeli konik kabuklar sadece doğrusal burkulma açısından değerlendirildikten sonra eğer yetişirse, son bölümde her ikisinin doğrusal-olmayan burkulma davranışlarının değerlendirilecektir.

Resim.1) Tip209-1.400 sınıfı denizaltıların mukavim tekneleri üzerinde kullanılan konik yapılar.
Kıçta düz kubbe ile sonlanan birden fazla simetrik konik yapı mevcut.
Başta ise yaklaşık 1,25D'lik bir sığ-küre kubbe ile nihayetlenen, dike yakın bir asimetrik koni tercih edilmiş.

Aslına bakılırsa sualtı uygulamalarında büyük ölçüde takviyeli konik kabuklar [Resim.1] kullanılır fakat konuya daha temelden bir giriş yapabilmek için takviyesiz konilerle başlamak daha mantıklıydı. Bu doğrultuda denel çalışmalara ait veriler çok önemli olduğundan kaynak [3] başlangıç noktası olarak seçildi ve burada deneyler için kullanılan geometri temel alındı.

Resim.2) Çalışmada kullanılan, Gmsh ile üretilen geometriler.

Söz konusu geometriyi ve sonlu elemanlar çözümleri için ihtiyaç duyulan hesaplama örgüsünü oluşturabilmek amacıyla açık-kaynak Gmsh [1] yazılımı kullanıldı. Böylece aşağıda verilen betik vasıtasıyla burada kullanılan önişlem malzemelerini konuyla ilgilenenlerin kolayca elde edebilmesi de mümkün hâle geldi.

 ♦ gmsh:
// Takviyesiz İnce Cidarlı Koni Burkulma Doğrulama Çalışması İçin
// Kaynak: Collapse and Buckling of Conical Shells, 2011
// J. Blachut - O. Ifayefunmi - M. Corfa
// Esneklik Katsayısı= 210,49GPa / Poisson Oranı= 0,281 / kalınlık= 0,002m
// Üsküdar Mühendishanesi - http://uskudar.biz
// Temel veriler
r1 = 0.074;  // küçük yarıçap, m
r2 = 0.099;  // büyük yarıçap, m
h0 = 0.100;  // yükselik, m
a0 = 0;      // eksen açısı, derece. 0 simetrik, (bu durum için) 14 dik koni
d0 = 36;     // çeyrek daire için düğüm sayısı
d1 = 26;     // uzunluk yönünde düğüm sayısı
// Eksen açısı için
z1 = h0*(Tan(a0*Pi/180));
// Noktalar
Point(1) = {0, 0, 0};    // merkez 1
Point(2) = {h0, 0, z1};  // merkez 2
Point(3) = {0, r2, 0};
Point(4) = {h0, r1, z1};
Point(5) = {0, 0, r2};
Point(6) = {h0, 0, r1+z1};
Point(7) = {0, -r2, 0};
Point(8) = {h0, -r1, z1};
Point(9) = {0, 0, -r2};
Point(10) = {h0, 0, -r1+z1};
// Çizgiler
  Circle(1) = {5,1,3};
  Circle(2) = {3,1,9};
  Circle(3) = {9,1,7};
  Circle(4) = {7,1,5};
  Circle(5) = {6,2,4};
  Circle(6) = {4,2,10};
  Circle(7) = {10,2,8};
  Circle(8) = {8,2,6};
  Line(9) = {3,4};
  Line(10) = {9,10};
  Line(11) = {7,8};
  Line(12) = {5,6};
// Yüzeyler
Line Loop(1) = {1,9,-5,-12};
  Surface(1) = {1};
Line Loop(2) = {2,10,-6,-9};
  Surface(2) = {2};
Line Loop(3) = {3,11,-7,-10};
  Surface(3) = {3};
Line Loop(4) = {4,12,-8,-11};
  Surface(4) = {4};
    Transfinite Line {1,2,3,4,5,6,7,8} = d0;
    Transfinite Line {9,10,11,12} = d1;
    Transfinite Surface "*";
    Recombine Surface "*";
// Örgü yüzey normallerini ters çevirmek için
// Burada kullanmak şart değildi ama ihtiyaç halinde faydalı olur...
Reverse Surface {1,2,3,4} ;  
// CalculiX için gerekli bâzı ayarlar
Mesh.SecondOrderIncomplete=1; // 2.derece elemanları doğru ihraç etmek için gerekli
Mesh.SaveGroupsOfNodes = 1;   // düğüm gruplarının kaydedilmesi için
Mesh.ElementOrder = 2;        // ikinci derece elemanlar için 2
// CalculiX için adlandırmalar
Physical Line("mesnet") = {1,2,3,4};
Physical Line("yuk") = {5,6,7,8};
Physical Surface("cidar") = {1,2,3,4};

Mevcut ayarlar ile bu betik 3.890 dörtgen hücreden meydana gelen ikinci derece bir düzenli örgü oluşturmaktadır ve eğer *.inp olarak ihraç edilirse, burada uygulandığı gibi, Calculix [2] ile doğrusal burkulma hesaplarını gerçekleştirmek için de kullanılabilir.

[3] içindeki denel ve hesaplamalı sonuçlarla karşılaştırma amacıyla orada tanımlanan 14° (dik) koni geometrisine eşdeğer bir yapı oluşturulmuş olmakla birlikte içerik biraz daha genişletildi.

[Resim.1] üzerinde görüldüğü gibi denizaltı mukavim tekneleri üzerinde bazen asimetrik koniler de kullanılabilmektedir. Bu sebeple verilen Gmsh betiği üzerine, simetrik koniye ilâve olarak asimetrik koni oluşturma imkânı da eklendi.

Böylelikle [3] üzerinde kullanılan simetrik koniye (a0=0°) ilave olarak, 3°, 6°, 10° ve 14° (dik koni) olarak dört farklı asimetrik konik kabuk daha oluşturularak [Resim.2] doğrusal burkulma davranışları incelendi. Calculix 2.14 ile elde edilen sonuçların özetleri aşağıda görülebilir...

Resim.3) 1e06Pa hidrostatik basınç altında Calculix-2.14 ile hesaplanan doğrusal burkulma katsayılarının ilk beş moda ait sonuçları. Gerçek burkulma sonuçlarının doğrusal yaklaşımla elde edilen değerlerin kabaca dörtte biri mertebesinde olacağını da dikkâte almak uygun olur.

Çizelge.1) Simetrik koni için hesaplanan hidrostatik burkulma sonuçlarının farklı eksen açılarına ait çözümlerle arasındaki farklar.
Görüldüğü gibi ilk mod için dik koni simetrik koniye göre %10,8 daha az yük taşıyabiliyor, en azından doğrusal açıdan...

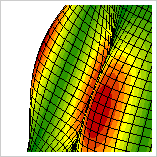
Resim.4) Simetrik (0derece) ve Dik (14derece) Koni için Calculix ccx ile hesaplanan 1. burkulma modları.
Sayısal değerler [Resim.3] üzerinde görülebilir.