Hem takviyeli hem de taksiyesiz silindirik kabuklar diğer pek çok alanda olduğu gibi Deniz Mühendisliği için de son derece önemli yapısal bileşenlerdir ve hemen her zaman basma yüklerine de maruz kaldıklarından burkulma kıstaslarına göre tasarlanmaları gerekir ve üstelik silindirlerin gösterdikleri burkulma davranışları levhaların ve daha önce ele alınan narin kirişlerin gösterdiklerinden bile daha şiddetli olarak gerçekleşir.

Mevzuya uzak olanlar için burkulma, inşa edilmiş güzelim bir simetrik yapıyı gizemli(!) bir şekilde bir anda hurdaya dönüştürebilme yeteneğine de sahiptir. Mühendisler burkulma ihtimâlini göz ardı ettiklerinde veya yeteri kadar dikkâtlice göz önüne almadan ya da alsalar bile hatalı yaklaşımlar kullanarak muhtelif tasarımlar ürettiklerinde önceki cümlede ifade edilen dönüşüm de gerçekleşebilir hâle gelmektedir ve hataya yatkın insan tabiatı göz önüne alındığında daima gelecektir denilebilir.

Bilhassa sualtı mühendisliğinde silindirik kabukların vazgeçilmez bileşenler olduğu göz önüne alınırsa bu yapıların burkulmaya olan hassasiyetleri de düşünüldüğünde silindir burkulması üzerinde çok dikkâtli bir şekilde durmak gerektiği rahatlıkla anlaşılabilir.

Konunun bu ilk bölümüne, göreceli kolay bir başlangıç yapabilmek için [1]'de yayınlanan bazı hesaplamalı ve denel çalışmaların sonuçlarını temel alıp aynı zamanda problemin en baştan ele alınarak ve tamamı açık kaynaklı dört yazılım; Gmsh[4], Elmer[5] ve Paraview[6] ile Gnumeric kullanarak tanımlanması, çözülmesi ve değerlendirilmesi ile elde edilen sonuçların yukarıda belirtilen kaynakta beyan edilen verilerle karşılaştırılması yoluna gidildi.

Çizelge.1) Kullanılan modellere ait hesaplamalar için gerekli temel fizikî veriler. Malzeme 6082-T6 Alüminyum ve borular dikişsizdir.

Böylece konuyla ilgilenmesi muhtemel mühendislerin ve mühendis adaylarının herhangi bir sıkıntı ile karşılaşmadan söz konusu yazılımları elde edebilmeleri ve hiçbir kısıtlama olmadan istedikleri gibi kullanabilmelerinin kolayca mümkün olduğunun gösterilmesi de ikincil bir hedef olarak sağlanabilecekti. Birkaç uluslararası ticarî yazılım kartelinin boyunduruğundaki Türkiye Cumhuriyetinin geleceği açısından bu husus aslında, maalesef başta üniversite camiaları olmak üzere pek çoklarının umurunda olmasa da hayâti bir öneme sahiptir.

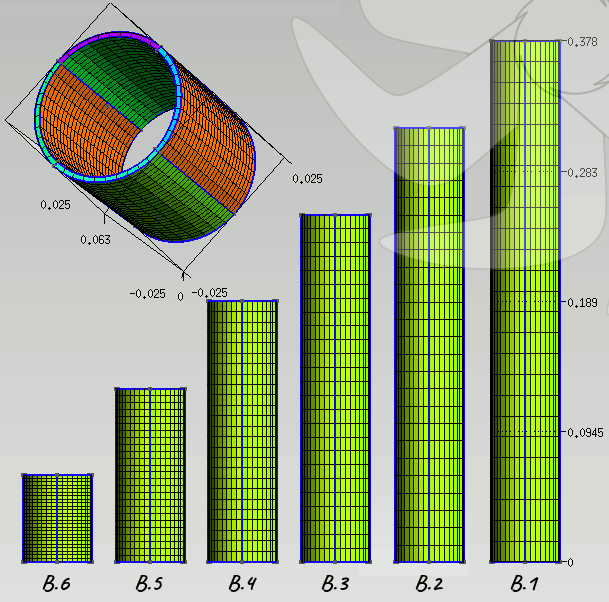
Resim.1) Takviyesiz silindirik kabukların burkulmasını incelemek amacıyla gmsh ile oluşturulan altı farklı model. Sonuçlar ticari bir yazılımla da karşılaştırılacağı için eleman sayısı bütün modellerde 1.000 adet olarak ayarlandı. Yaşanan bazı sorunlardan dolayı B.6 için farklı bir hesaplama örgüsü daha kullanıldı.

Kaynak [1]'de takip edilen denel ve hesaplamalı yaklaşımlarla uyumlu olabilmek için [Çizelge.1] ve [Çizelge.2]'de belirtilen fizikî niteliklere sahip eşdeğer kesitte ve altı farklı uzunluktaki silindirler için [Resim.1]'de gösterilen düzenli örgü yapısında ve 1.000 altıyüzlü hücreden müteşekkil altı adet hesaplama örgüsü imâl edildi.

Söz konusu belgenin temel konusu yukarıda tanımlanan ölçülerdeki dikişsiz Alüminyum boruların hidrostatik basınç altındaki çökme davranışı sonuçlarının elde edilmesine dayanmaktadır. Ayrıca problemin hem analitik hem de ticarî bir yazılım kullanılarak Doğrusal (Euler) Yaklaşım ile çözülmesine ait sonuçlar mevcuttur.

Bu ilk bölümde Elmer ile elde edilen Euler Burkulması değerleri hem von Misses (Analitik) hem de Ansys (Euler) çözümleri ile karşılaştırılacaktır.

Asıl önemli olan mevzu olan gerçek deney sonuçları ile karşılaştırmanın Doğrusal Olmayan Plastik çözüm gerektiren, çok daha karmaşık fizik modellerine ihtiyaç gösteren ikinci bölümde ele alınması düşünülmektedir.

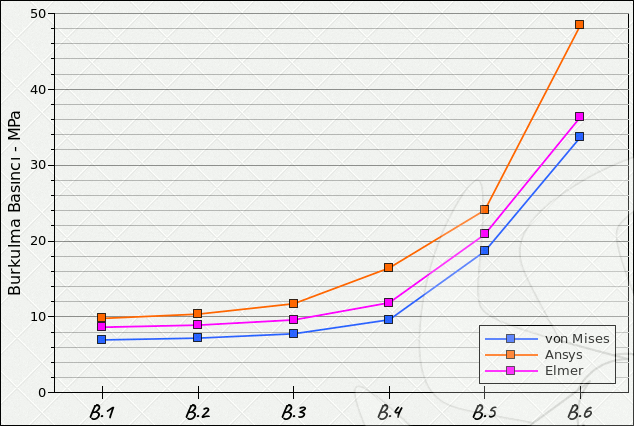
Çizelge.2) [1]'den alınan von Mises[e.1] ve Ansys sonuçları ile Elmer'in karşılaştırılması. Grafik için [Resim.2]

Konuyla ilgili en eski analitik çözümlerden olan von Mises eşitliği aşağıdaki gibidir;

[1]'de sunulan verilerdeki sonlu eleman çözümü için kullanılan yaklaşım 1.000 civarında, 8 düğümlü ve ikinci derece Shell93 2B kabuk elemanına dayanmaktadır. Buradaki hesaplamalarda Elmer için kullanılan yaklaşımda ise yine 1.000 adet ama 3B hacim elemanı; ikinci derece (820) kullanılmıştır. Elde edilen sonuçların özeti ve diğer sonuçlarla karşılaştırılması [Çizelge.1] ve [Resim.2] üzerinde görülebilir. Boruların her iki ucu da, deney modellerine uygun olarak, dönmeye serbest olacak şekilde mesnetlenmiştir.

Resim.2) Doğrusal (Euler) Burkulama için Elmer ile edilen sonuçların son derece başarılı olduğu söylenebilir.

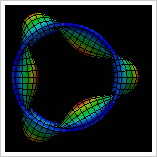
Resim.3) B.1 ve B.6 Modelleri için elde edilen, Hidrostatik Yük altındaki doğrusal burkulma şekilleri.

Karşılaşılan Bazı Sorunlar:

1. B.6 üzerinde gerçekleştirilen ilk çözümde yapı üzerinde bazı dengesizlik sorunları ortaya çıktı ve hatalı sonuçlar elde edildi. Bütün borular için tek örgü çözünürlüğü kullanıldığı için [Resim.1] üzerinde de görülebileceği üzere altıyüzlü hesaplama hücresi için Yan Oranı (Uzunluk/Genişlik) 1'in altına indiğinden dolayı böyle bir sorun ortaya çıkmış olabilir gibi gözüktüğünden B.6 için uzunluk doğrultusunda çözünürlük azaltılarak ve Yan Oranı 2'ye yükseltilerek sorun düzeltildi.
2. B.5 modeli için elde edilen ilk moda ait n sayısı 3 olarak gerçekleşti. Fakat ikinci mod için gerçekleşen n 2 oldu ki biraz ters bir durum. Bu sorunun temel sebebi tam anlaşılamamış olsa da daha önceki Kalın Cidarlı Silindir Doğal Frekansı hesaplamalarında karşılaşılan frekansların doğru olmasına rağmen mod şekillerinde safha kayması yaşanmasına benzer bir durum gibi gözüktü, bu sorunun kaynağı henüz tespit edilemedi.

Elmer için cidar modellenmesinde kullanılabilecek 2B kabuk elemanları, en azından şimdilik oldukça kısıtlı seçenekler sunmaktadır. Henüz geliştirme aşamasında olan "ShellSolver" çözücüsü belli bir olgunluk seviyesine ulaşmadığından şimdilik silindir 3 Boyutlu hacim elemanlarıyla modellendi.

Konun devamında burada kullanılan temel modellerin Doğrusal Olmayan Burkulma davranışlarının, yapı üzerindeki geometrik kusurların da meseleye dâhil edilerek, incelenmesi ve yine [1]'deki denel verilerle karşılaştırılması söz konusu olabilir...