Gemi Mühendisliği sahasında dalgalar ve bilhassa kırılan dalgalar çok önemli çalışma alanlarını teşkil etmektedir. Dalgalar deniz araçlarının direnci üzerinde doğrudan etkili olduğu gibi gerek askeri uygulamalar için dikkate alınması gereken izler gerekse tabiat üzerindeki etkiler açısından da son derece önemlidir.

Bu makale ile başlayan yazı dizisi ile önce serbest su yüzeyi dalgaları, ikinci olarak kırılan dalgalar ve eğer fırsat olursa son olarak sualtı dalgalarının öncelikle RANS olmak üzere çeşitli Hesaplamalı Akışkan Dinamiği yaklaşımları ile incelenmesi ve elde edilen bazı verilerin konuya ilgi duyabilecek ziyaretçilere sunulması hedeflenmektedir.

Bugün için standart RANS¹ yaklaşımları ile serbest yüzeyi şekillerinin ve ilk dalga çukurunun konumunun ve derinliğinin hassas olarak tespit edilebilmesinde yetersizlikler mevcuttur ve BEM² gibi türbülans modellemesi içermeyen yöntemlerin böyle çözümler için hassasiyetleri daha iyidir. RANS yöntemlerinde karşılaşılan sıkıntının temel kaynaklarından biri olarak kullanılan türbülans modellerinin ürettiği yüksek seviyede girdap kıvamlılığı gösterilebilir.

Diğer taraftan LES³ ve belki DES⁴ yaklaşımları ile bu tür sıkıntıların üstesinden gelmek de mümkün olabilir gibi görünse de bu defa da hesaplama maliyetlerinin çok yükseleceğini göz önünde bulundurmak icâb eder, özellikle gerçek Reynolds ve Froude sayılarında deniz araçlarının modellemeleri söz konusu olduğunda.

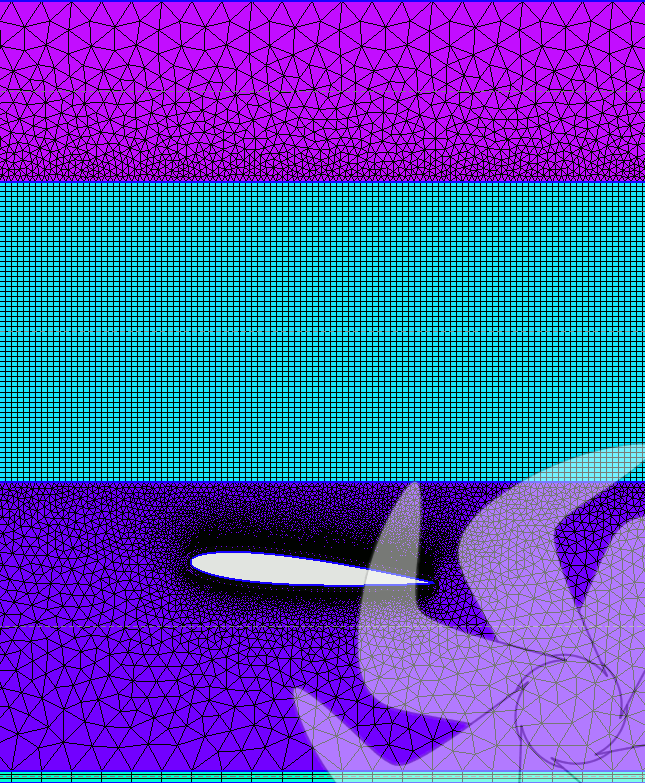
Resim.1) Duncan deney ortamının benzetimi amacıyla Gmsh ile oluşturulan melez hesaplama örgüsünün kanat civarındaki görünüşü. Kanat kesiti Naca0012, HA= 5derece.

Araştırmacılar için dalmış durumdaki cisimlerin serbest su yüzeyinde oluşan dalga izlerinin sayısal olarak kestirilmesi, gerçekleşen kaldırma ve direnç kuvvetlerinin hesaplanmasından daha önemli bulunmaktadır. Dolayısıyla su-hava arayüzündeki etkileşimlerin incelenmesine yönelik olarak uzun senelerdir deney havuzlarında gerçekleştirilen pek çok tecrübî çalışamalar ve elde edilen veriler günümüz sayısal çalışmalarının da temelini oluşturmaktadır.

İlk olarak ele alınacak veriler Duncan (1983) tarafından gerçekleştirilen deneylere ait ölçümlere dayanacaktır. Kırılan dalgalara sıra geldiğinde, ayrıca diğer bazı deneyler de ele alınabilir. Duncan'ın makalesinde [1] çeşitli hücum açıları, akış hızları ve kanat su çekimlerine göre elde edilen deney ölçümlerine ait veriler mevcuttur. Deney verilerinin hassasiyeti ±0.3cm olarak belirtilmiştir ki başka bir ifadeyle azami dalga yüksekliğinin yaklaşık %19'una kadar sapmalar söz konusu olabilir.

Çizelge.1) Deney ortamını meydana getiren temel veriler.
(*) Daha farklı HA, Fr ve d değerleri ile yapılmış ölçümler de mevcut olmakla birlikte Üsküdar Mühendishanesi tarafından gerçekleştirilen benzetimlerde sadece yukarıdaki değerler kullanılmıştır.

Söz konusu çalışmada dalga ölçüm verileri çizelge ile değil de grafik olarak sunulduğu için mevcut çizimlerden bir şekilde verilerin geri kazanılması da gerekmektedir. Bu iş için ben hemen daima g3data kullanıyorum ve şiddetle tavsiye ederim. Fakat bu şekilde gerçekleştirilecek bir veri kazanımı ile birlikte Duncan'ın belirttiği ölçüm belirsizliği sınırı olarak beyan edilen ±0.3cm'in biraz daha artacak olması da kaçınılmazdır.

Çeşitli araştırmacılar Duncan'ın deney sonuçlarını farklı sayısal yaklaşımlara elde etmeye çalışagelmektedir. Bunlar arasında en bilinenleri olarak Landrini'nin (1999) ve Faltinsen ile Semenov'un (2008) Sınır Elemanları Yöntemi ile yaptığı ve dalga kırılması başlangıcına kadar olan şartlar için hassas çözümler elde edebildikleri çalışmalar gösterilebilir.

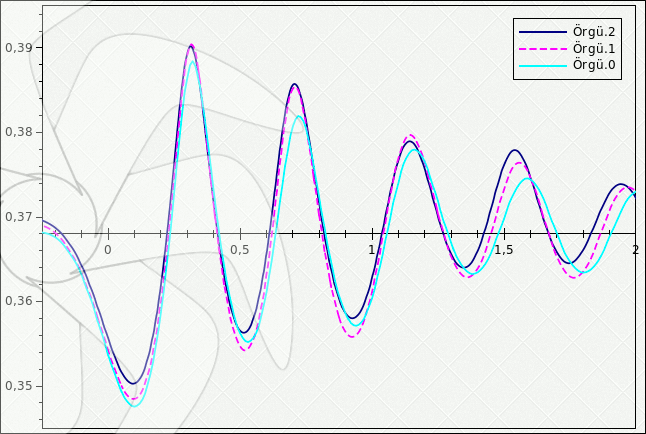
Resim.2) 0,193m (d/c=0,951) su çekiminde hesaplamalarda kullanılan üç farkı örgü çözünürlüğüne ait sonuçların karşılaştırılması.

Bu çalışmada kullanılan ve tamamı açık kaynaklı olan yazılımlar şöyledir:

1. Önişlem: Gmsh 2.10.1
2. Hesaplama: OpenFOAM 2.3.1
3. Sonişlem: Paraview 4.1.0 | Gnumeric 1.12.9 | g3data 1.5.2

Yukarıda da kısaca değinildiği gibi RANS yaklaşımları ile ise henüz sadece kısmen başarılı sonuçlar elde edilebilmiştir. RANS yöntemleri genellikle doğru dalga şekillerini üretebilmekle birlikte çoğunlukla dalga genliklerini daha düşük hesaplama ve takip eden dalgalarının çok hızlı sönümlenmesi gibi sorunlara maruz kalmaktadırlar. Hemen yukarıdaki [Resim.2] k-ω SST modeli kullanılarak elde edilen çözümlerde söz konusu sönüm davranışını açıkça göstermektedir. Diğer taraftan bu husus ikinci bölümde ayrıntılı olarak ele alınacaktır.

İlave olarak özellikle dalga kırılma bölgeleri için ampirik verilere dayanan (Cointe ve Tulin, 1994) bazı kırılan-dalga modellerinin ilavesi ile özellikle kırılma bölgelerinin daha iyi hesaplanabildiğini ifade eden çalışmalar da vardır.

Çizelge.2) Benzetimler için oluşturulan üç farklı çözünürlükteki hesaplama alanlarını oluşturan hücre sayıları.

İlk safhada doğal olarak deney ortamını ifade eden 2B hesaplama örgüsünün imalâtı gerçekleştirilmiştir. Mükemmel bir açık kaynak yazılım olan Gmsh ile şimdilik serbest ve düzenli örgülerin bir arada bulunduğu melez bir örgü yapısı inşa edilmiş [Resim.1] ve örgü temel olarak beş farklı bölgeye ayrılmıştır.

1. Dalgaların oluşacağı suhattı bölgesi için elde edilebilecek azami dalga genliklerine uygun yükseklikte bir düzenli örgü bölgesi.
2. Kanat çevresinde sınır tabakanın daha iyi çözülebilmesi için uygun kalınlıkta bir düzenli örgü bölgesi.
3. Taban bölgesinde sınır tabakanın daha iyi çözülebilmesi ve incelenebilmesi için alçak bir düzenli örgü bölgesi.
4. Ve bütün bu bölgeleri birbirine bağlayan iki serbest örgü bölgesi.

Örgü boyutlarına olan hassasiyeti de incelemek gerekeceğinden üç farklı çözünürlük uygulanmıştır. Üretilen örgülere ait hücre sayıları [Çizelge.2]'de görülebilir. Bütün diğer değişkenler eşdeğer olmak kaydıyla, kOmegaSST türbülans modeli ile gerçekleştirilen karşılaştırma sonucunda [Resim.2]'de görülen sonuç elde edilmiştir.

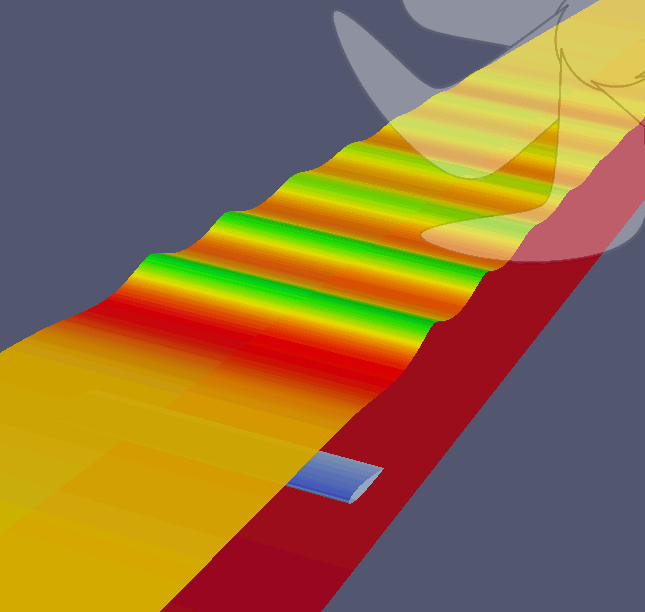
Resim.4) Mevcut kurulum şartlarında d/c=0,951, Fr=0,567 için elde edilmiş bir sonişlem görüntüsü. Ayrıntılı veriler ve deney sonuçlarıyla karşılaştırmalar sonraki bölümde yayınlanacak...

Şimdiye kadar [Çizelge.2]'de tanımlanan üç farklı örgü ve [Çizelge.1]'de belirtilen deney şartları kullanılmak suretiyle elliden fazla çözüm gerçekleştirilerek muhtelif model değişkenlerinin ve sınır şartlarının hesaplama sonuçları üzerindeki etkisini anlamaya yönelik veriler elde edildi. Bütün verilerin değerlendirilerek anlaşılabilir bir hale getirilmesinden sonra takip edecek bölümlerde sunulması söz konusu olacaktır diye ümit ediyorum...

İkinci Bölüm: Serbest Su Yüzeyi Fiziğinin HAD ile İncelenmesi - VoF