|
 OpenFOAM bugün için en geniş kullanıcı kitlesine sahip açık kaynaklı hesaplamalı akışkan dinamiği yazılımı olarak, gelişmesini ve yayılmasını yüksek bir ivme ile sürdürmektedir. Bunun temel sebebi sunduğu çok geniş hesaplama imkânlarının yanında açık kaynaklı olması ile kullanıcıların kendi ihtiyaçlarına göre tamamen uyarlanabilir ve geliştirilebilir bir mimariye sahip olmasıdır. Tabii ki lisans maliyetinin sıfır olması da son derece önemlidir. OpenFOAM bugün için en geniş kullanıcı kitlesine sahip açık kaynaklı hesaplamalı akışkan dinamiği yazılımı olarak, gelişmesini ve yayılmasını yüksek bir ivme ile sürdürmektedir. Bunun temel sebebi sunduğu çok geniş hesaplama imkânlarının yanında açık kaynaklı olması ile kullanıcıların kendi ihtiyaçlarına göre tamamen uyarlanabilir ve geliştirilebilir bir mimariye sahip olmasıdır. Tabii ki lisans maliyetinin sıfır olması da son derece önemlidir.
Avrupa kaynaklı bu yazılım gerek Avrupa ülkeleri ve Uzak Doğu gerekse 3.Dünya ülkelerinde hem akademik hem de ticari çevrelerde çok geniş bir kullanıma ulaşmış durumdadır ve yaygınlaşmaya da devam etmektedir. Türkiye'de ise (ABD'ye paralel olarak!) durum maalesef bu gidişatın tersi yönündedir. Bunun temel sebebinin Türk akademik çevrelerinin büyük ölçüde ithâl ticari yazılım pazarlamacılarının kıskacında olmasından kaynaklandığı düşünülebilir.
Bu sayfada OpenFOAM ile yapılan bazı denemelerle ilgili veriler paylaşılacaktır. Daha önce bahsi geçen bir kamasalma kesitinin incelenmesi mevzusu OpenFOAM vasıtasıyla RANS1 yaklaşımı ile ve birkaç türbülans modeli için yüksek-Re hesaplama örgüsü kullanılarak karşılaştırılmaya ve değerlendirilmeye çalışılacaktır.
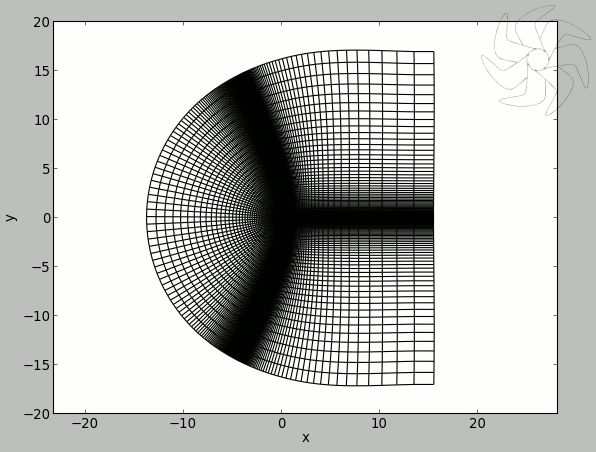
Resim.0) naca 64a413 kanat kesiti etrafında oluşturulan 2B düzenli C-Örgü.
Hesaplama örgüsü Re=3,198e06 için, yArtı=100 civarında bir değer verecek şekilde açık kaynaklı Construct2D tarafından üretilmiştir (resim.0) ve bütün türbülans modelleri için aynı örgü kullanılmıştır. Elde edilen düzenli C örgüsü 34.551 dörtgen elemandan müteşekkildir. OpenFOAM çok çeşitli türbülans modellerine sahip olup ilave olarak kullanıcıların kendi türbülans modellerini oluşturabilmelerine de olanak sağlamaktadır.
Çalışmanın bu ilk bölümde duvar fonksiyonları kullanılarak yüksek-Re çözümler elde edebilmek için üç türbülans modeli seçilmiştir;
- SpalartAllmaras
- kOmegaSST
- realizableKE
Ayrıca dördüncü olarak panel yöntemi kullanan xFoil ile de çözüm elde edilip bir karşılaştırma yapılacaktır. Kullanılan temel sınır şartları çizelge.1'de, elde edilen bazı temel değerler ise çizelge.2'de görülebilir. Her üç türbülans modeli için de aynı rahatlatma katsayıları kullanılmış ve çözümler 3.000 tekerrüre kadar sürdürülmüştür.
| Kanat Kesiti |
naca 64a413 |
| Kesit Uzunluğu |
650 mm |
| Akış Hızı - u |
5 m/s |
| Hücum Açısı - alfa |
0 derece |
| nCrit |
9 |
| Türbülans Yoğunluğu - TU |
%0,07 |
| Türbülanslı Uzunluk Ölçeği - l |
0,17C |
| Türbülans Kinetik Enerjisi - k |
1,837e-05 |
| Türbülans Sönüm Oranı - epsilon |
6,415e-08 |
| Özgül Sönüm Oranı - omega |
3,879e-02 |
| Türbülanslı Kinematik Kıvamlılık - nut |
1,06e-07 |
| Kinematik Kıvamlılık - nu |
1e-06 |
| Çözücü |
simpleFoam |
Çizelge.1) Benzetimler için kullanılan temel sınır şartları.
|
spalartAllmaras |
kOmegaSST |
realizableKE |
xFoil |
| Hesaplama Süresi * |
519 saniye |
740 saniye |
666 saniye |
~1 saniye |
| yArtı - asgari |
21,5 |
19,6 |
17,8 |
- |
| yArtı - azami |
122,8 |
112,6 |
113,2 |
- |
| yArtı - ortalama |
90 |
79 |
75 |
- |
| Girdaplılık - azami |
13.311 |
11.958 |
12.092 |
- |
| Basınç Katsayısı - azami |
1,344 |
0,992 |
0,992 |
0,999 |
| Basınç Katsayısı - asgari |
-0,477 |
-0,482 |
-0,493 |
-0,497 |
Çizelge.2) Elde edilen bazı veriler.
* Alttaki muhtelif eğrilerden de anlaşılabileceği gibi aslında çözümler 1.000 tekerrür civarında dengelenmiş gibi olduğundan yukarıdaki hesaplama sürelerinin sadece 1/3'ünde bir ölçüde sonuca ulaşıldığı varsayılabilir. Yine de çözümler 3.000 tekerrüre kadar sürdürülmüştür.
|
spalartAllmaras |
kOmegaSST |
realizableKE |
| nut |
nutUSpaldingWallFunction |
nutUSpaldingWallFunction |
nutUSpaldingWallFunction |
| k |
- |
kqRWallFunction |
kqRWallFunction |
| epsilon |
- |
- |
epsilonWallFunction |
| omega |
- |
omegaWallFunction |
- |
Çizelge.3) Türbülans modelleri için kullanılan OpenFOAM duvar fonksiyonları.
Çizelge.4) Bu çalışma için kullanılan temel yazılımlar ve donanım. Problemin küçüklüğü sebebiyle paralel hesaplama uygulanmamış ve bütün çözümler için işlemcinin altı çekirdeğinden biri kullanılmıştır. İşletim sistemi dahil kullanılan bütün yazılımlar açık kaynaklıdır!
Elde edilen sonuçlar fazla lâfa ihtiyaç duyulmadan aşağıdaki resimler vasıtasıyla kolayca anlaşılabilir. Yine de kısaca birkaç hususa değinmek faydalı olabilir.
- Çözümler durağan hâl2 için elde edildiğinden SIMPLE3 algoritması kullanılmıştır. Daha sonra geçici hâl4 için PIMPLE ile de benzer bir çalışma yapıp durumu karşılaştırmak düşünülebilir.
- Hesaplamalar 2B ortamda yapılmıştır. Bu durumda daha yüksek hesaplama örgüsü çözünürlüğü ve daha yüksek yArtı değerleri kullanılabilirdi. Yine de ilk aşamada bu değerler kısmen düşük tutulmuştur çünkü ortalama bir bilgisayar ortamında 3B model kullanıldığında makûl olarak kullanılabilecek çözünürlük ve yArtı değerlerinin bu mertebelerde olması beklenebilir (en azından benim bilgisayar için) ve bu sebeple tercih edilen türbülans modellerinin bu örgü çözünürlüğü ve y+ seviyesindeki davranışları hakkında fikir sahibi olmak daha sonraki muhtemel 3B çalışmalar açısından faydalı olabilecektir.
- Çizelge.2'de görülebileceği gibi panel yöntemi ile RANS yöntemi arasında hesaplama süreleri arasında çok büyük bir fark mevcuttur buna rağmen elde edilen sonuçlar açısından xFoil'in gayet başarılı iddia edilebilir. Üstelik bu sürelere RANS yöntemi için gereken oldukça uzun önişlem ve sonişlem zamanları dahil bile değildir.
- Naca 64a413 bir laminar akış kesiti olduğu için laminar-türbülans geçiş bölgesinin oldukça geride ortaya çıkacaktır. xFoil bu geçiş bölgesini emme yüzü için 0,706, basma yüzü için 0,584 civarında tahmin etmiştir. Elde bunu doğrulayacak bir rüzgar tüneli verisi olmamasına rağmen mevcut sınır şartları için bu değerler makûl gibi görünüyor.
- Diğer taraftan kullanılan RANS yöntemi ve türbülans modelleri, beklendiği üzere herhangi bir geçiş bölgesi tespit edemedi. RANS'ın ve mevcut türbülans modellerinin bu konudaki sıkıntılarının üstesinden gelebilmek için çok daha düşük yArtı değerlerine (yArtı ≤ 1) ve sınır tabakayı duvar fonksiyonları kullanmadan çözebilecek düşük-Reynolds türbülans modellerine ihtiyaç vardır. Sonraki safhalarda bu yönde bir inceleme daha yapılması düşünülmektedir.
- İkinci safhada farklı örgü çözünürlükleri ile aynı problem çözülmeye çalışılacaktır ve böylece burada elde edilen değerlerin örgüye olan hassasiyeti biraz daha iyi anlaşılabilir. Üçüncü safhada farklı yArtı değerleri ile çözümlerin karşılaştırılması düşünülmektedir. Dördüncü safhada düşük-Re modelleri ile denemeler yapılabilir...
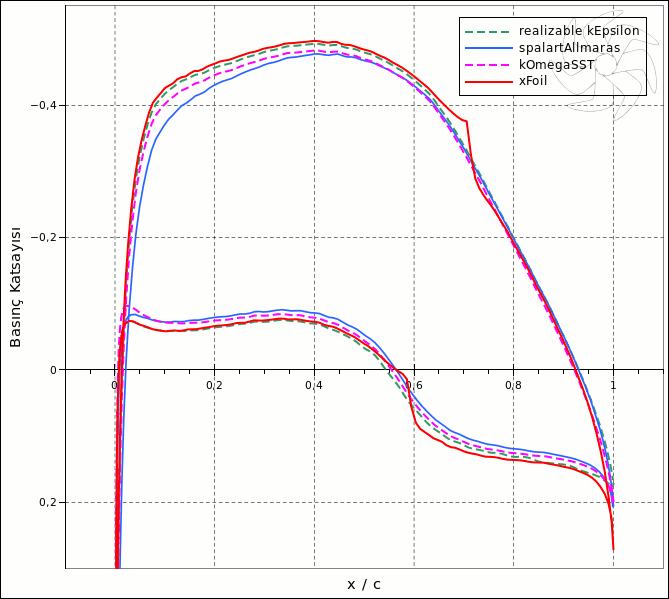
Resim.1) Dört yöntemle naca 64a413 kanat kesiti üzerinde elde edilen basınç dağılımları.
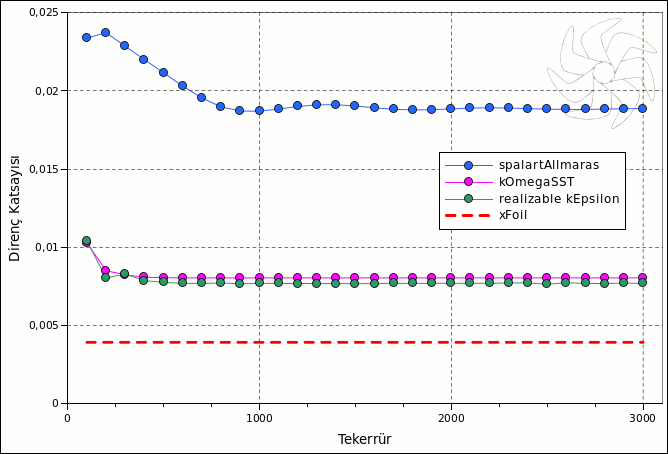
Resim.2) Dört yöntem ile naca 64a413 için elde edilen direnç katsayıları.

Resim.3) Dört yöntem ile naca 64a413 için elde edilen kaldırma katsayıları.
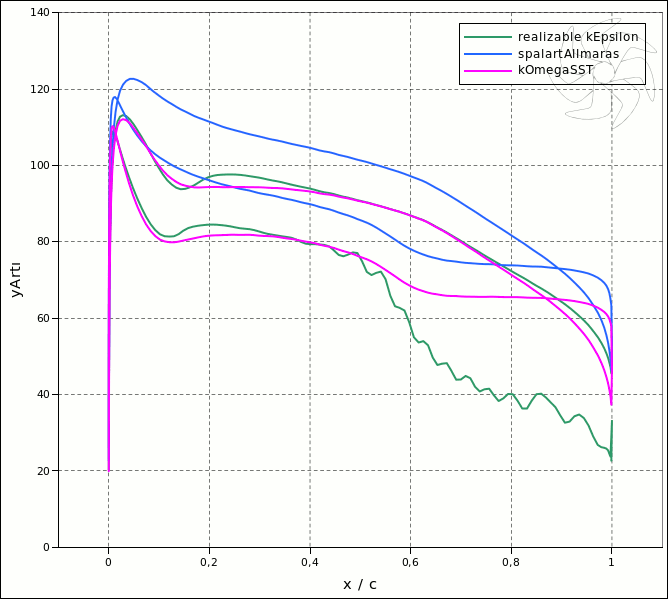
Resim.4) Aynı hesaplama örgüsü üzerinde eşdeğer sınır şartları kullanıldığında kesit üzerinde oluşan boyutsuz yArtı değerlerinin dağılımları.
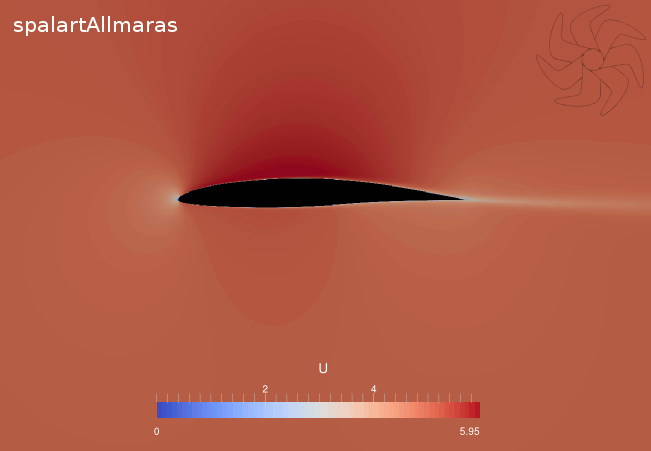
Resim.5) SpalartAllmaras için naca 64a413 kesiti etrafındaki bileşke akış hızı büyüklüğü.

Resim.6) realizable kEpsilon türbülans modeli için naca 64a413 kesiti çevresinde oluşan dinamik basınç.

Resim.7) kOmegaSST türbülans modeli için naca 64a413 kesiti çevresindeki türbülans kinetik enerjisi.
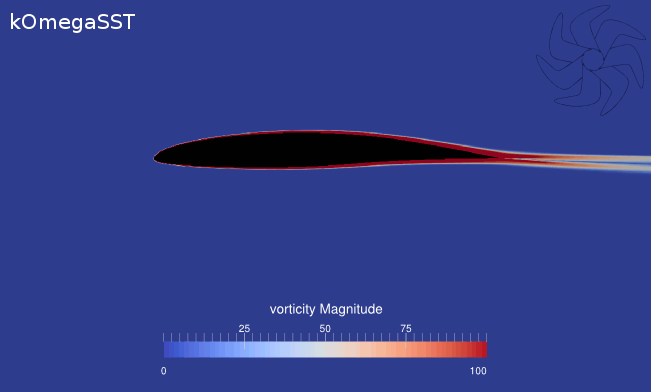
Resim.8) kOmegaSST türbülans modeli için naca 64a413 kesiti çevresindeki girdaplılık büyüklüğü.
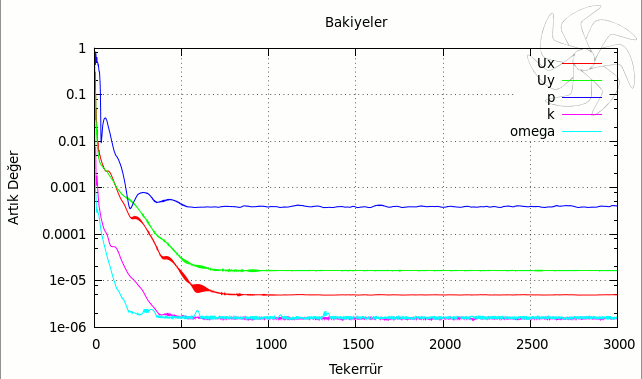
Resim.9) kOmegaSST türbülans modeli için çözüm sürecindeki artık değerler.
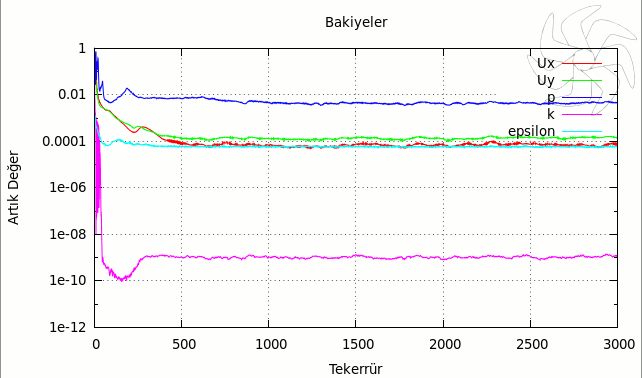
Resim.10) realizable kEpsilon türbülans modeli için çözüm sürecindeki artık değerler.
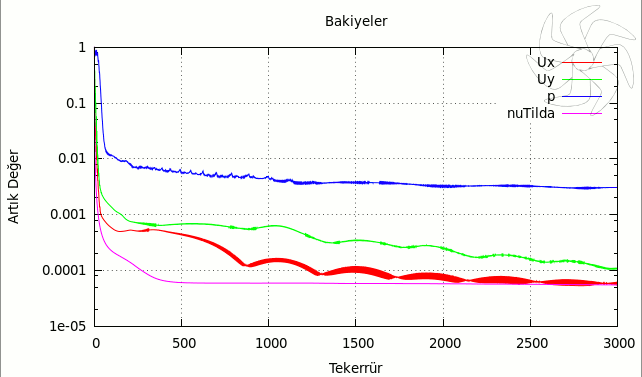
Resim.9) SpalartAllmaras türbülans modeli için çözüm sürecindeki artık değerler.
Takip eden incelemelerde y+ ve örgü çözünürlüğü gibi değişkenlerin burada özet olarak sunulan sonuçlar üzerindeki etkileri belki ilgi çekici olabilir:
- SpalartAllmaras türbülans modelinin muhtelif yüksek-Re yArtı değerlerine bağlı davranışı
- kOmegaSST türbülans modelinin muhtelif yüksek-Re yArtı değerlerine bağlı davranışı
- realizableKE türbülans modelinin muhtelif yüksek-Re yArtı değerlerine bağlı davranışı
- SpalartAllmaras türbülans modelinin yArtı=100 civarındaki üç farklı örgü çözünürlüğüne bağlı davranışı
|












