Basınç taşıyan yapıların tasarımında çok önemli bir yeri olan küre temelli cisimlerin burkulma davranışları hakkındaki temel bir giriş, yarıküre üzerinden önceki bölümde ele alınmıştı. Şimdi küre kökenli bir başka cisim olan elipsoitler bu açıdan incelenecektir.

Gerçek kürenin eksenlerden biri doğrultusunda uzatılması veya basılması ile elde edilen ve bu sebeple uzatılmış küre ve basık küre olarak da adlandırılan, eksenel simetriye sahip, elips kesitlerinden meydana gelen bu tür cisimler de yük altında ince cidarlı taşıyıcı yapılar imâl etme yönünde önemli seçeneklerden birini meydana getirmektedir.

Şimdilik konu yine sadece doğrusal (Euler) burkulma yaklaşımı kullanılarak ele alınacak. Daha önce açıklandığı üzere bu yöntem ile gerçekçi burkulma değerlerine yaklaşabilmek mümkün olmasa da muhtelif benzer geometrilerin nicelik değil ama nitelik açısından bir karşılaştırmasını yapabilmek mümkün olabilir, acaba bu varsayım geçerli mi?

Bu sorunun cevabını belki daha sonra alabileceğiz. Şimdilik adım adım ilerlemek daha iyi. Bu kez analitik çözüm ile uğraşmadan doğrudan hesaplamalı çözüme ulaşmak tercih edildi. Dolayısı ile önce hesaplama örgüleri oluşturmak, sonra çözmek ve nihayet alınan sonuçları değerlendirmek gerekecek.

Kullanılacak yazılımlar önişlem için Gmsh (3.0.6) çözüm için CalculiX ccx (2.13) ve sonişlem için de CalculiX cgx (2.13) ve gnumeric (1.12) olacak.

Resim.1) Aşağıda verilen parametrik Gmsh betiği ile oluşturulan 1:0,5R elipsoit yüzey modeli ve örgüler.
Sağ altta görülen örgü betik içindeki "Recombine" komutu (satır.37) ile soldaki üçgen temelli serbest örgüden, dörtgen temelli serbest örgüye dönüştürülerek elde edildi. Bu tür yüksek eğriliğe sahip cisimler üzerinde 2.derece örgü kullanmak şart.

Hesaplama amacıyla tek eksen üzerinde basılmış ve uzatılmış küre geometrileri değerlendirilecek. Bu amaçla birkaç satırdan meydana gelen aşağıdaki parametrik gmsh betiği (*.geo) rahatlıkla kullanılabilir. Söz konusu betik vasıtasıyla Gmsh'ye yabancı olanlar bile kolayca istedikleri hesaplama örgülerini üretebilir ve uygun şekilde ihraç ederek buradaki gibi CalculiX veya herhangi başka bir sonlu eleman çözücüsünde kullanabilir. Fakat mevzunun fazla uzamaması için şimdilik ihraç edilen örgünün çözücülere ithâl edilmesi konusu ele alınmayacak.

 ♦ gmsh:
// Eliptik-Kürevî kubbeler için serbest örgü
// Üsküdar Mühendishanesi - http://uskudar.biz
// temel değişkenler
r0 = 3.1125;  // esas yarıçap, metre
or = 0.50;  // elips eksen oranı, küre için 1.0
lc = 0.14;  // eğriler üzerindeki düğüm sayılarının ayarlanması için
 
// buradan sonrasını ellemeye pek gerek yok
r2 = or*r0;  // elips ikinci yarıçap 
 
// noktalar
Point (1) = {0, 0, 0};    // merkez noktası
Point (2) = {0, 0, r2, lc};  // dikey yarıçap
Point (3) = {r0, 0, 0, lc};  // yatay yarıçap
Point (4) = {0, r0, 0, lc};
 
// eğriler
  Ellipse (1) = {3,1,3,2};
  Ellipse (2) = {4,1,4,2};
  Circle (3) = {3, 1, 4};
 
// yarım cisim için çeyrek yüzey modeli (1/8 elipsoit yüzeyi)
Line Loop(200) = {2,-1,3};
  Ruled Surface(200) = {200};
 
// mevcut yüzeyin kopyalanarak çoğaltılması
  Rotate { {0, 0, 1}, {0, 0, 0}, Pi/2 } 
        { Duplicata { Surface {200}; }  
       }
  Rotate { {0, 0, 1}, {0, 0, 0}, -Pi/2 } 
        { Duplicata { Surface {200}; } 
        }
  Rotate { {0, 0, 1}, {0, 0, 0}, Pi/2 } 
        { Duplicata { Surface {201}; } 
        }
 
Recombine Surface "*"; // üçgen temelli örgüyü serbest dörtegene dönüştürmek için
 
// CalculiX için gerekli bâzı ayarlar
Mesh.SecondOrderIncomplete=1; // 2.derece elemanları doğru ihraç etmek için gerekli
Mesh.SaveGroupsOfNodes = 1;  // düğüm gruplarının kaydedilmesi için
Mesh.ElementOrder = 2;     // ikinci derece elemanlar için 2
 
// CalculiX için adlandırmalar
Physical Line("mesnet") = {3,204,208,212}; 
Physical Surface("kafa") = {200,201,205,209};

İlk bölümdeki yarıküre geometrisi için düzenli örgü kullanılmıştı. Şimdi ise birkaç farklı sebeple serbest örgü tercih edildi. İki yöntem arasında yapılan karşılaştırmaya ait bâzı temel veriler [Çizelge.1] üzerinde görülebilir.

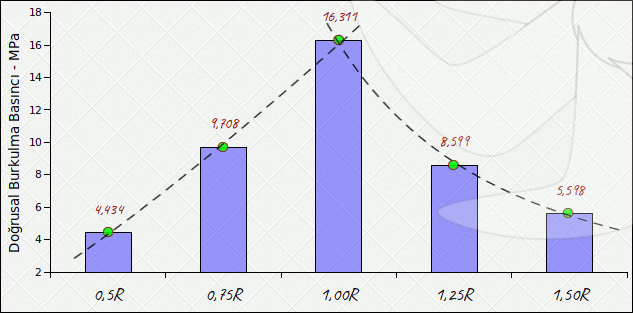
Çizelge.1) Mevcut betik ile 1:1R elipsoit başka bir ifadeyle küre için elde edilen serbest örgüler ile yapılan bâzı hesaplamaların önceki bölümde düzenli örgü kullanılarak gerçekleştirilen durum ile karşılaştırılması.
Bu değerlendirme sonucunda eliptik hesaplamalara ikinci derece S8R elemanı ve serbest örgü kullanılarak devam edilmesine karar verildi.

Hesaplamalar için beş farklı kafa örgüsü meydana getirildi. 1:1,0R (betik içinde or=1,0) yarıküre geometrisini, 0,50R ve 0,75R basık küre geometrisini, 1,25R ve 1,50R de uzatılmış küre geometrisini temsil etmektedir. R temel yarıçaptır ki 3,1125m'dir. Ve nihayet malzeme daha önce olduğu gibi HY80, et kalınlığı 25mm olarak belirlenmiştir. Elde edilen sonuçların özeti [Resim.2] üzerinde ve birkaç ayrıntı [Resim.3 ve 4] üzerinde görülebilir.

Resim.2) Muhtelif elipsoitler üzerinde hesaplanan kritik doğrusal burkulma değerleri.
1,00R yarıküre durumudur. Sol tarafı meydana getiren basık küre ve sağ tarafı meydana getiren uzatılmış küre durumlarının eğilimleri dikkât çekici.

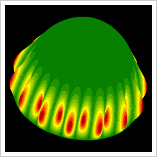
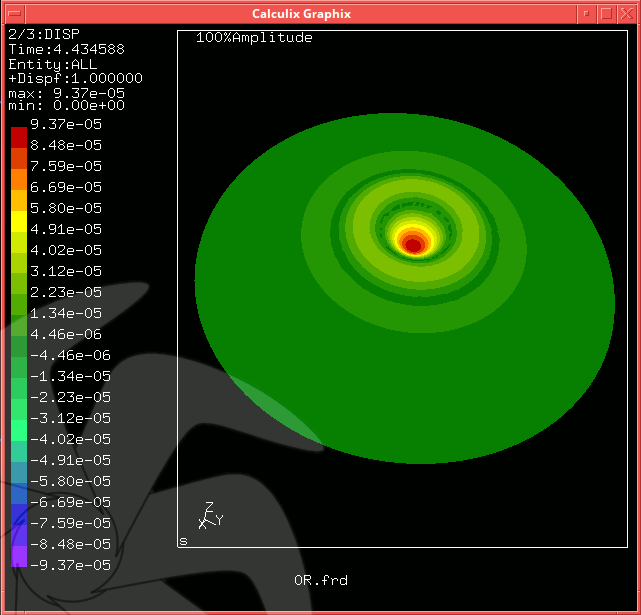
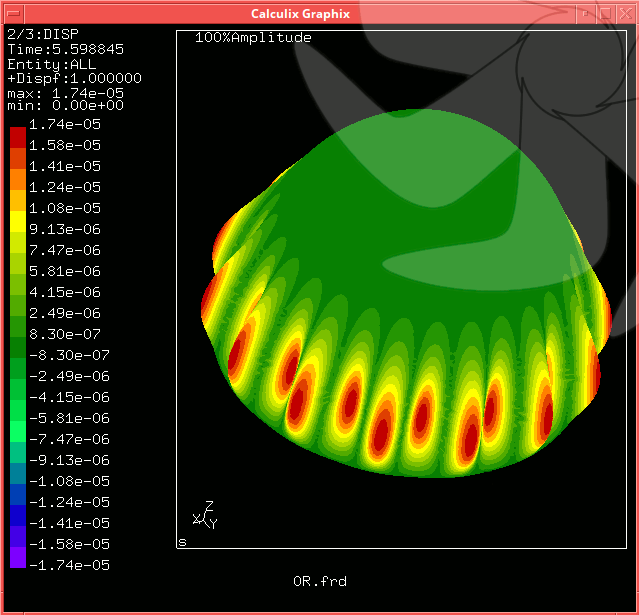
Resim.3, 4) 0,5R ve 1,5R durumları için Calculix ile hesaplanan ilk burkulma modları.

Tâkip edecek inceleme muhtemelen sığ küreler ve ayrıca geometrik kusurların burkulma davranışı üzerindeki etkileri hakkında olacak gibi görünüyor...