Akışhattı eğriliği ve dönme etkisindeki türbülanslı akışlar, türbülansı arttıran veya azaltan ilâve kuvvetlere mâruz kalırlar. Türbülans seviyeleri üzerindeki eğrilik ve dönme kaynaklı değişikler bu tür akışları ve bilhassa da laminer-türbülans geçiş oluşumunu belirgin derecede etkiler. Boussinesq varsayımını temel alan Girdap Lüzûciyeti Modeli (GLM) basitlik ve kararlılık özellikleriyle günümüzün mühendislik benzetimlerinde yaygın olarak tercih edilmektedir.

Bununla birlikte GLM'ler akışhattı eğriliğine ve dönmeye karşı duyarsızdır. Üstelik türbülans eşyönlülüğü varsayımı sebebiyle türbülanslı akış içinde dönme etkisini tanımlamak da zordur ve Coriolis kuvvetinin tahrik ettiği doğrusal olmayan dalganın etkisi altında akışın yapısı değişebilmektedir.

Sonuç olarak GLM yaklaşımlarının kullanıldığı RANS benzetimlerinde gerekli düzeltmelerin uygun bir şekilde yapılması ihtiyacı vardır. Konuyla ilgili çalışmalar göstermiştir ki eğriliğin yönü akış üzerindeki etkiler açısından en baskın değişkendir. Dışbükey eğrilik türbülans kinetik enerjisini ve kayma gerilmelerini azaltmak suretiyle türbülansı bastırır başka bir ifadeyle dengelerken içbükey eğrilik tam tersine türbülansı arttırır, dengesizleştirir.

Son birkaç senedir RANS yaklaşımlarını dönme/eğrilik etkileri altındaki akışlarda daha etkin olarak kullanabilmek için bu yönde yapılan çalışmalar giderek artmaktadır. Doğrusu bu çalışmalar gemi mühendisliği için de son derece önemlidir çünkü bu mühendislik sahasında karşılaşılan RANS temelli çözüm ihtiyaçlarının pek çoğu için dönme ve eğrilik düzeltmesi ihtiyacı elzemdir.

Şimdilik burada Spalart-Allmaras modeli için geliştirilmiş bâzı dönme/eğrilik düzeltmesi modellerinin düzeltilmemiş modellerle karşılatırılmasıyla elde edilmiş ilk veriler özet olarak sunulacaktır. SA yanında piyasada yaygın olarak kullanılan mesela iki eşitlikli k-ε ve k-ω türevi modeller için de dönme/eğrilik düzeltmelerine ihtiyaç vardır.

Bu değerlendirmede aşağıdaki Spalart-Allmaras türbülans modeli uyarlamaları (3,4 ve 5 dönme/eğrilik düzeltmesi içerir) açık kaynaklı OpenFOAM 2.3.1 kullanılarak kısaca değerlendirilmeye çalışılacaktır:

1. SA-fv3: Uzun zamandan beri OpenFOAM sürümlerinde kullanılan öntanımlı Spalart-Allmaras uyarlaması fv3 terimine sahip bu sürümdür. Tercih edilmesinin temel sebebi olarak özellikle karmaşık 3B yapılar üzerinde standart Spalart-Allmaras (SA) sürümüne göre daha kararlı çalışması gösterilmektedir. Oluşturulması modeli geliştirenler ile uyarlamayı yapanlar arasındaki özel yazışmalarla gerçekleştiğinden model resmi olarak yayınlanmış bir makaleye dayanmaz. Alışılmadık geçiş davranışı sebebiyle alçak Reynolds sayılarında bu modelin kullanılması tavsiye edilmemektedir.
2. SA-neg: 2012 tarihli makale [1]'e dayanan ve negatif SA olarak adlandırılan bir uyarlamadır. Kaynak kodu [3]'den alınabilir ve oradaki tanımlaması SpalartAllmaras2012'dir. Bu modeli kullanabilmek için derlemeniz gerekir. Model hakkında daha fazla bilgi için [2] incelenebilir.
3. SA-RC.0: Bu modeli kullanabilmek için kaynak kodunu [4]'ten alıp derlemeniz gereklidir. Standart SA sürümüne sıkıştırılamaz akışkanlar için Spalart-Shur [5] Dönme/Eğrilik Düzeltmesi ilâvesiyle elde edilmiştir. Kaynak sitede yayınlanan verilere göre en iyi sonucun alındığı belirtilen [Cr1=1,0 - Cr2=12,0 - Cr3=1,0] sabitleriyle kullanılmıştır.
4. SA-RC.1: Bu modelin kaynak kodu [3]'den alınabilir; oradaki tanımlaması SpalartAllmaras2012SARCM'dir ve kullanabilmek için derlemeniz gerekir. Üstteki 3. modelden farklı olarak standart SA değil SA-neg temel alınarak oluşturulmuş bir diğer Dönme/Eğrilik Düzeltmesi modelidir ve söz konusu düzeltme [6]'ya dayanmaktadır. Model sabitleri olarak ön tanımlı [Cr1=1,0 - Cr2=2,0 - Cr3=1,0] değerleri kullanılmıştır.
5. SA-RC.2: Yukarıdaki SA-RC.1 modelinin Qiang ve Yong [6] tarafından tavsiye edilen [Cr1=1,0 - Cr2=12,0 - Cr3=0,6] sabitleriyle kullanılmış hâlinden ibârettir.

NACA0012

2 Boyutlu ilk safha karşılaştırmada zaten üzerinde çalışılmakta olduğu için elde yeterince hazır verinin mevcut olduğu naca0012 incelenecektir. Asıl hedef 3 Boyutlu akış olduğu için burada sunulan veriler sınırlı tutulmuştur. Sonuçlar aşağıdaki resimler vasıtasıyla kolayca anlaşılabilir. Naca0012 çalışmasının başlangıç verileri için OpenFOAM NACA0012'ye Karşı - SpalartAllmaras sayfası incelenebilir. Bütün türbülans modelleri için elde edilen sonuçlar birbirlerine gâyet yakındır. Yine de eşdeğer şartlar altında yakınsama davranışları arasında bâzı farklar mevcuttur. Yakınsama davranışı açısından modeller en hızlıdan en yavaşa doğru;

1. SA-RC.1
2. SA-neg
3. SA-RC.0
4. SA-RC.2
5. SA-fv3

olarak sıralanmıştır.

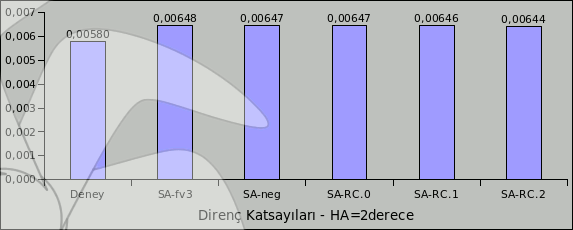
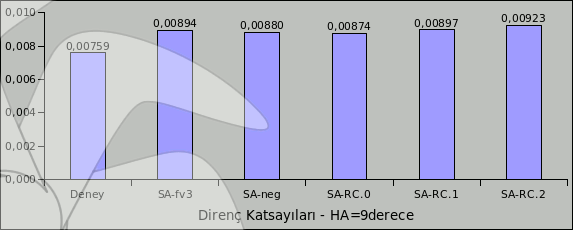
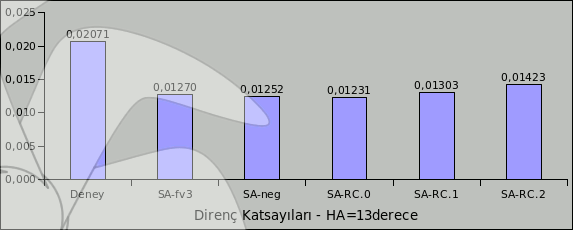
Resim.1-2-3) Ele alınan türbülans modelleri ile nacac0012 için elde edilen direnç katsayıları.

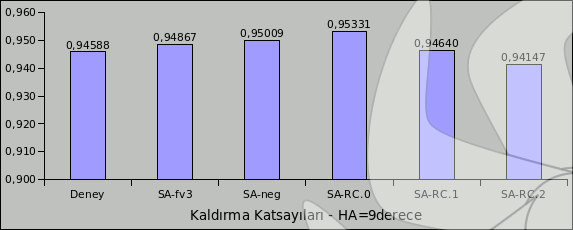
Resim.4) Ele alınan türbülans modelleri ile nacac0012 için 9derece'de elde edilen kaldırma katsayıları.

6:1 Uzatılmış Küre

3 Boyutlu ilk karşılaştırma için daha önce üzerinde çalışmış olan bu cisim tercih edilmiştir. Ayrıntılı bilgiye 6:1 Uzatılmış Küre için HAD İncelemeleri - 20derece sayfasında ulaşılabilir. Akışhattı eğriliği üzerinde bir karşılaştırma yapabilmek için bu cisim gâyet uygun olarak kabûl edilebilir. Geometrinin tanımlanması açısından son derece kolay olsa da özellikle 20derecelik hücum açısı için etrafında oluşan akış son derece karmaşık ve zorludur.

Bahsi geçen ilk çalışmada SA türbülans modeli oldukça yetersiz kalmıştı fakat söz konusu çalışma sadece yüksek-Re türbülans modellerini karşılaştırmak için gerçekleştirildiğinden SA'nın da duvar fonksiyonlarıyla kullanıldığını göz ardı etmemek gerekir ki böyle yüksek seviyede ayrılmış bir akış için duvar fonksiyonların yetersiz kalması beklenebilirdi. Şimdiki çalışmada da deney sonuçlarıyla değil de yukarıda açıklanan beş farklı SA uyarlamasının birbirleriyle karşılaştırılması hedeflendiğinden yine duvar fonksiyonları kullanılmıştır.

3B için modellerin yakınsama davranışları 2B naca0012'den farklılık göstermiştir. Yakınsama davranışı açısından modeller en hızlıdan en yavaşa doğru;

1. SA-RC.0
2. SA-fv.3
3. SA-neg
4. SA-RC.2
5. SA-RC.1

olarak sıralanmıştır. Fakat aradaki farklar oldukça küçüktür.

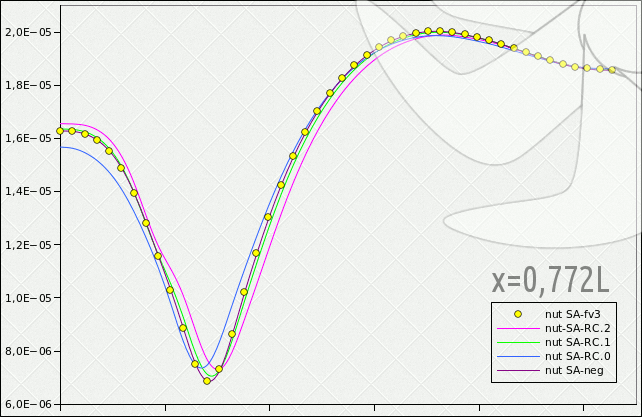
Resim.5) X=0,772L düzleminde beş farkı SA uyarlaması için elde edilen kinematik türbülanslı lüzûciyet (ν_t) değerlerinin kesit etrafındaki dağılımları. Bâzı modeller arasında beklendiği gibi belirgin farklar var. Bu arada SA-fv3'ün SA-neg ile eşdeğer sonuç verdiği açıkça ortadadır.

Resim.6) x=0,772L kesiti üzerinde cismin rüzgâraltı bölgesinde hesaplanan basınç değerleri. En iyi sonuç SA-RC.2 olsa da aslında deney verilerinden gâyet uzak. Fakat daha uygun örgü, yArtı ve sınır şartları ile gelişme sağlanabilir. Bir Dönme/Eğrilik düzeltme modeli olmasına rağmen SA-RC.0'ın en kötü sonucu vermesi de ilgi çekici!

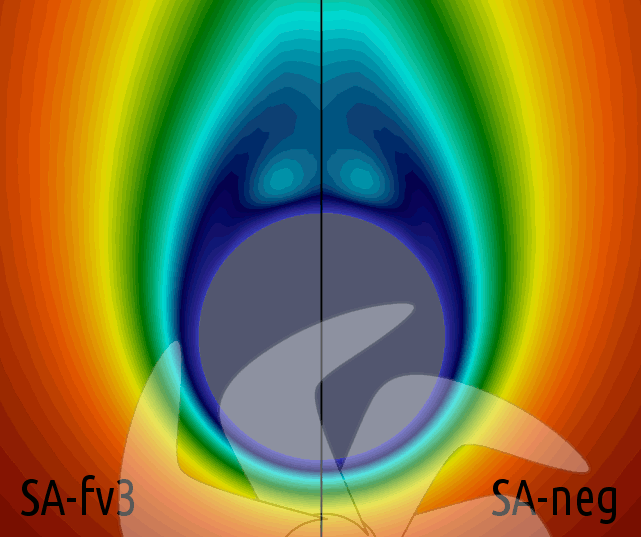
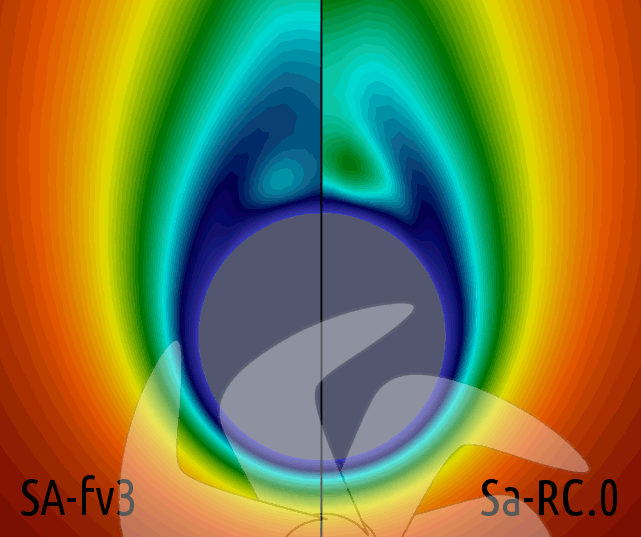
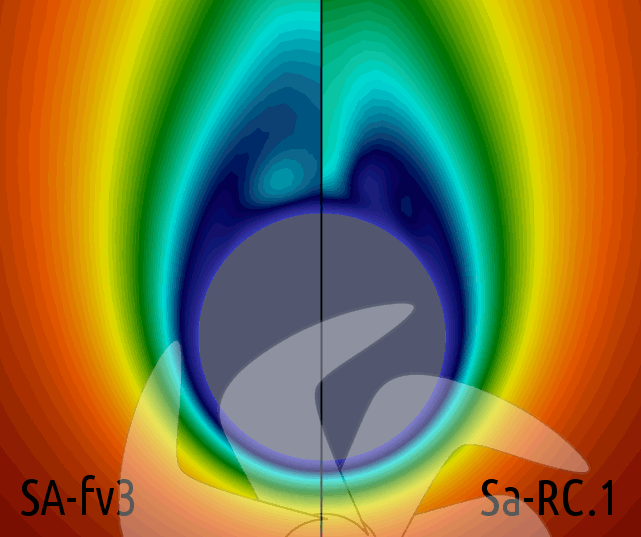
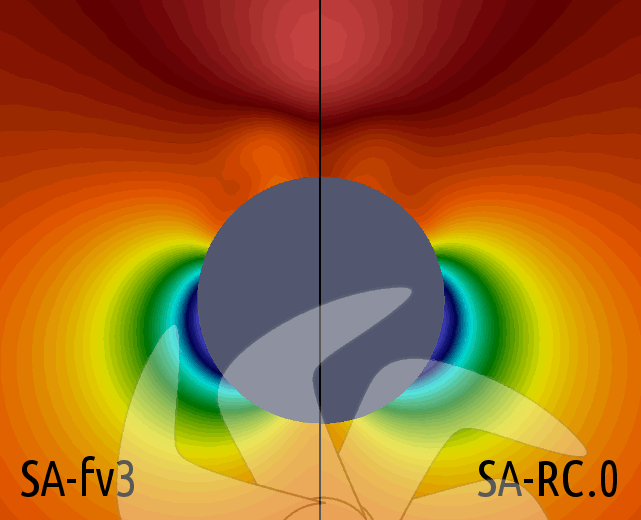
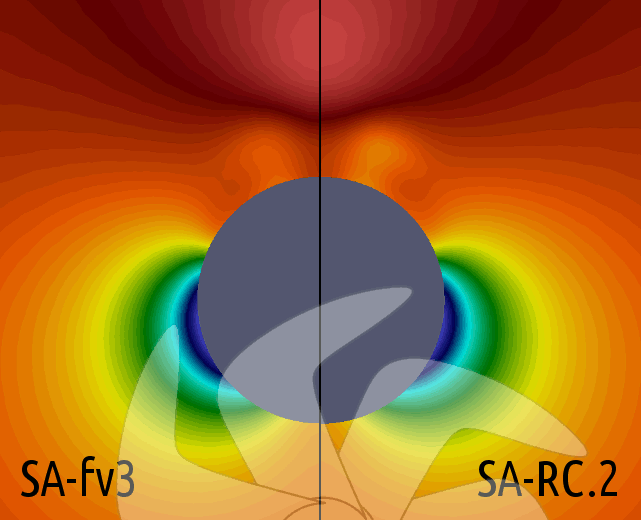
Resim.7-8-9-10) x=0,772L düzleminde, ele alınan bütün türbülans modelleri için hesaplanan kinematik türbülanslı lüzûciyet (ν_t) değerlerinin OpneFOAM için öntanımlı uyarlama olan SA-fv3 ile karşılaştırmaları.

Resim.11-12) x=0,772L düzleminde SA-RC.0 ve SA-RC.2 modellerine ait basınç (P) sonuçlarının SA-fv3 ile karşılaştırılması.

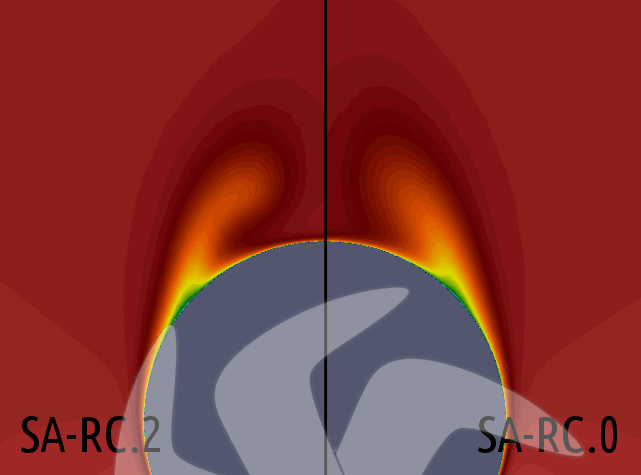
Resim.13) x=0,772L düzleminde SA-RC.2 ve Sa-RC.0 için hesaplanan Ux değerlerinin karşılaştırılması.

Dönme/Eğrilik düzeltmesi ile alâkalı ilk değerlendirme bundan ibâret. Tabii şimdilik sadece eğrilik düzeltmesinin etkisini kısmen inceleyebilmek mümkün oldu ve dönme etkisi incelenemedi. Yine de buradan elde edilen verilerle ikinci safhada daha kapsamlı bir değerlendirme yapabilmek belki bir gün mümkün olabilir.

Bir diğer dikkât çekici sonuç OpenFOAM'da kullanılan ve NASA'nın sitesinde kullanılması tavsiye edilmez şeklinde bir ibâre bulunan SA-fv3'ün SA-neg ile karşılaştırıldığında büyük ölçüde eşdeğer sonuçlar verebilmesinden de anlaşılabileceği gibi aslında yerinde bir tercih olduğudur. Unutmamak gerekir ki burada ele alınan 2B ve 3B modeller geometrik olarak gâyet kolaydır ve çok daha karmaşık geometriler üzerinde fv3 uyarlaması kullanmak daha da mantıklı bir hâle gelebilir...