|
 Ortalama bir Hesaplamalı Akışkan Dinamiği çalışması söz konusu olduğunda, sınırı tabakayı daha iyi çözebilmek için duvar yakınındaki kısıtlı bir bölge için düzenli, geri kalan hesaplama ortamı için ise serbest örgü kullanarak her iki yaklaşımın üstünlüklerinden birlikte yararlanmaya çalışmak yaygın bir uygulamadır. Ortalama bir Hesaplamalı Akışkan Dinamiği çalışması söz konusu olduğunda, sınırı tabakayı daha iyi çözebilmek için duvar yakınındaki kısıtlı bir bölge için düzenli, geri kalan hesaplama ortamı için ise serbest örgü kullanarak her iki yaklaşımın üstünlüklerinden birlikte yararlanmaya çalışmak yaygın bir uygulamadır.
Böyle bir melez örgü, her ne kadar burada örnek olarak kullanılacak geometri kolay sayılsa da tam düzenli örgü oluşturmanın son derece zaman alıcı ve zorlu olabildiği karmaşık cisimler üzerinde daha verimli çalışabilmeyi mümkün kılabilmektedir.
Daha önce ele alınan düzenli örgü üretimi hakkındaki içeriğe de iyi uyum sağlayabilmek ve mevzû ile ilgilenenlerin yöntemler arasındaki farklıları daha kolay kavrayabilmelerine yardımcı olabilecek şekilde bir bütünlük sağlayabilmek için yine aynı 6:1 Uzatılmış Küre hendesesi ile devam edilecektir.

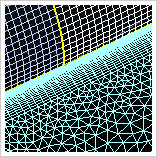
Resim.1) 2 Boyutlu eksensimetrik melez hesaplama örgüsün.
Aşağıda verilen Gmsh betiğini olduğu gibi kopyalayıp "deneme2Bmelez.geo" veya keyfinize göre başka bir isim verilmiş metin dosyası içine yapıştırıp bu dosyayı Gmsh ile açtığınızda yukarıda bahsi geçen cisim için OpenFOAM'a yönelik olarak oluşturulmuş 2 Boyutlu bir eksensimetrik hesaplama örgüsünü elde edebilirsiniz.
Önceki yazıda söz konusu örgünün Gmsh'den nasıl ihraç edilip daha sonra OpenFOAM içine nasıl ithâl edileceği anlatıldığı için bu hususlar şimdi tekrar edilmeyecek...
♦ gmsh: // 6:1 "Uzatılmış Küre" (elispsoit) geometrisi ve OpenFOAM için // 2B eksensimetrik hesaplama örgüsü oluşturma betiği numunesi // Prismatik sınır tabaka katmanı ile melez örgü oluşturma // Üsküdar Mühendishanesi - http://uskudar.biz // Temel veri girişi r1 = 0.2; // kısa yarıçap, metre - eliposit çapı = 0,4m oran1 = 6; // elips çap oranı - elipsoit uzunluğu = 2,4m oran2 = 23; // sınır yarıçapının cisim uzunluğuna oranı // Noktalar vasıtasıyla eğriler üzerindeki // düğüm sayılarını belirleyen değişkenler lc1 = 0.004; lc2 = 1.0; lc3 = 2.0; // Buradan sonrasına müdahale etmeye gerek yok! r2 = oran1 * r1; // uzun yarıçap R1 = oran2 * r2; // uzak alan sınırı yarıçapı // y+ için kerteriz // Re=4,2e06 - L=2,4m - y+=50 için deltay=0.0007544; // y+ ~50 için ilk hücrenin duvara mesafesi, metre Point(999)= {0, r1+deltay, 0, 1}; // y+ ~50 için vasatta kerteriz noktası Point(0) = {0, 0, 0}; // merkez noktası Point(1) = {-r2, 0, 0, lc1}; Point(2) = {0, r1, 0, lc1*3}; Point(3) = {r2, 0, 0, lc1}; Point(4) = {-R1, 0, 0, lc2}; Point(5) = {R1, 0, 0, lc2}; Point(6) = {0, R1, 0, lc3}; Ellipse(10) = {1,0,1,2}; // sol çeyrek Ellipse(11) = {3,0,3,2}; // sağ çeyrek Circle(20) = {4,0,6}; // sol çeyrek Circle(21) = {6,0,5}; // sağ çeyrek Line(30) = {1,4}; // sol eksen hattı Line(31) = {3,5}; // sağ eksen hattı // Yüzey Line Loop(50) = {10,-11,31,-21,-20,-30}; Plane Surface(100) = {50}; // Sınır Tabaka Field[1] = BoundaryLayer; Field[1].EdgesList = {10,11}; // sınır tabakanın uygulanacağı kenarlar Field[1].NodesList = {1,3}; // sınır tabakanın sonlanağı düğüm noktaları Field[1].hwall_n = 0.00065; // ilk hücrenin yüksekliği Field[1].thickness = 0.05; // toplam düzenli örgü kalınlığı Field[1].ratio = 1.10; // hücreler arası mesafe artış oranı Field[1].Quads = 1; BoundaryLayer Field = 1; // Oluşturulan 2B yüzeyin -2,5derece döndürülmesi için. // Dönüş açıları gmsh'ye radyan olarak verilmeli! Rotate { {1,0,0} , {0,0,0} , -Pi/72 } { Surface{100}; } // Döndürülmüş yüzeyin +5derece çekilerek düzenli örgünün elde edilmesi // Böylece aşağıda Layers komutu ile tanımlandığı üzere {1} hücre // genişliğinde "sahte 3B" bir hesaplama hacmi oluşturulabiliyor. Extrude { {1,0,0} , {0,0,0} , Pi/36 } { Surface{100}; Layers{1}; Recombine; } // OpenFOAM için isimlendirmeler Physical Volume ("hava") = {1}; Physical Surface ("cisim") = {110,113}; Physical Surface ("girişÇıkış") = {117,120}; Physical Surface ("iskele") = {122}; Physical Surface ("sancak") = {100};
Sıfırdan farklı hücum açılarında da akışı inceleyebilmek için gerekli olan 3 Boyutlu hesaplama örgüsü de yukarıdaki betiğin hafifçe değiştirilmesi ile kolayca edilebilirdi. Aşağıdaki resimde de görülebildiği üzere yarım küre şeklindeki bir hesaplama hacimi içinde oluşturulan simetrik yapı çoğu durum için ihtiyacı karşılamaya yeterli olacaktır.

Resim.2) 3 Boyutlu simetrik (yarım) melez hesaplama örgüsü.
Bazı durumlarda ise tam küre bir hesaplama ortamı gerekli olabilir ki mevcut betik üzerine yapılacak küçük bâzı ilâvelerle bu ihtiyaç da kolayca karşılanabilir.
Velhâsıl aşağıdaki betik "deneme3Bmelez.geo" gibi bir düz metin dosyası içine yapıştırılarak kolayca kullanılabilir.
♦ gmsh: // 6:1 "Uzatılmış Küre" (elispsoit) geometrisi ve OpenFOAM için // 3B hesaplama örgüsü oluşturma betiği numunesi // Prismatik sınır tabaka katmanı ile melez örgü oluşturma // Üsküdar Mühendishanesi - http://uskudar.biz // Temel veri girişi r1 = 0.2; // kısa yarıçap, metre - eliposit çapı = 0,4m oran1 = 6; // elips çap oranı - elipsoit uzunluğu = 2,4m oran2 = 23; // sınır yarıçapının cisim uzunluğuna oranı // Noktalar vasıtasıyla eğriler üzerindeki // düğüm sayılarını belirleyen değişkenler lc1 = 0.004; lc2 = 1.0; lc3 = 2.0; // Çap yönündeki düğüm noktası sayısı dr = 24; // her çeyrek daire için! // Buradan sonrasına müdahale etmeye gerek yok! r2 = oran1 * r1; // uzun yarıçap R1 = oran2 * r2; // uzak alan sınırı yarıçapı // y+ için kerteriz // Re=4,2e06 - L=2,4m - y+=50 için deltay=0.0007544; // y+ ~50 için ilk hücrenin duvara mesafesi, metre Point(999)= {0, r1+deltay, 0, 1}; // y+ ~50 için vasatta kerteriz noktası Point(0) = {0, 0, 0}; // merkez noktası Point(1) = {-r2, 0, 0, lc1}; Point(2) = {0, r1, 0, lc1*3}; Point(3) = {r2, 0, 0, lc1}; Point(4) = {-R1, 0, 0, lc2}; Point(5) = {R1, 0, 0, lc2}; Point(6) = {0, R1, 0, lc3}; Ellipse(10) = {1,0,1,2}; // sol çeyrek Ellipse(11) = {3,0,3,2}; // sağ çeyrek Circle(20) = {4,0,6}; // sol çeyrek Circle(21) = {6,0,5}; // sağ çeyrek Line(30) = {1,4}; // sol eksen hattı Line(31) = {3,5}; // sağ eksen hattı // Yüzey Line Loop(50) = {10,-11,31,-21,-20,-30}; Plane Surface(100) = {50}; // Sınır Tabaka Field[1] = BoundaryLayer; Field[1].EdgesList = {10,11}; // sınır tabakanın uygulanacağı kenarlar Field[1].NodesList = {1,3}; // sınır tabakanın sonlanacağı düğüm noktaları Field[1].hwall_n = 0.00065; // ilk hücrenin yüksekliği Field[1].thickness = 0.05; // toplam düzenli örgü kalınlığı Field[1].ratio = 1.10; // hücreler arası mesafe artış oranı Field[1].Quads = 1; BoundaryLayer Field = 1; // 2B örgü yüzeyi ile iki yönde çekilerek iki çeyrek küreden oluşan // 3B hesaplama ortamının elde edilmesi Extrude { {1,0,0} , {0,0,0} , Pi/2 } { Surface{100}; Layers{dr}; Recombine; } Extrude { {1,0,0} , {0,0,0} , -Pi/2 } { Surface{100}; Layers{dr}; Recombine; } // OpenFOAM için isimlendirmeler Physical Volume ("hava") = {1,2}; Physical Surface ("cisim") = {110,113,132,135}; Physical Surface ("girişÇıkış") = {117,120,139,142}; Physical Surface ("merkez") = {122,144};
Bu şekilde elde edilebilecek olan örgü de daha önce 2B için açıklandığı gibi kolayca OpenFOAM içine ithâl edilebilir. Doğal olarak bâzı yamaların türleri farklı olacaktır.
Tam bu noktada küçük bir düzeltme yapmaya ihtiyaç olacaktır. Genel olarak OpenFOAM utf-8 isimlendirmelerle bir sorun çıkarmadığı için türkçeye özgü harflerin kullanılması da bir soruna sebep olmaz. Bununla birlikte polyDualMesh kullanıldığında bu durum geçerli değil. Bu sebeple ikinci betik üzerindeki 74. satırda görüldüğü üzere "girişÇıkış"olarak adlandırılmış yamanın içindeki Ç, ı ve ş harfleri polyDualMesh aracının çalışmasına engel olmaktadır ki bu sebeple söz konusu aracı kullanmadan önce gerekli noktalar üzerinde bu yamanın adını mesele girisCikis olarak düzeltmeniz gerekecektir...
Elde edilen bu üç boyutlu melez [Resim.2] hesaplama örgüsü duvar civarında düzenli bunun dışındaki hacim içinde ise serbest türdedir. Bu serbest örgüyü meydana getiren bileşenler üçgen temelli (dörtyüzlü ve beşyüzlü) hücrelerdir, sınır tabaka örgüsünü meydana getiren bileşenler ise dörtgen temelli (altıyüzlü) hücrelerdir.

Resim.3) 3 Boyutlu simetrik (yarım) melez; çokgen ağırlıklı hesaplama örgüsüden bir kesit.
OpenFOAM sahip olduğu bâzı ilâve yeteneklerle, Gmsh üzerinde imâl edilerek ithâl edilen bu melez örgü içindeki üçgen temelli elemanların çokgen temelli olanlara dönüştürülebilmesine de imkân sağlamaktadır. Bu işlemi gerçekleştirebilmek için polyDualMesh adlı araç kullanılır. Çalışma dizininin kökünde şöyle:
♦ Uçbirim: polyDualMesh 45 -overwrite
Böylece üçgen ağırlıklı örgü çokgen ağırlıklı [Resim.3] bir hâle de dönüştürebilir. Her iki yaklaşımın çözüm süreleri ve yakınsama davranışları üzerindeki etkisini incelemek ise şimdilik daha müsâit bir zamana kalsın...
Son olarak yukarıda verilen betik ayarları ile elde edilen üçgen örgü ile doğrudan bundan dönüştürülmüş çokgen örgü arasındaki temel yapı farkını ifade etmek gerekirse:
|
üçgen |
çokgen |
| noktalar |
761.976 |
1.247.284 |
| yüzler |
3.126.346 |
2.761.121 |
| dâhili yüzler |
3.060.086 |
2.710.497 |
| hücreler |
1.177.824 |
761.976 |
| hücre başına yüz |
5,25 |
7,18 |
|
| altıyüzlü |
310.464 |
322.414 |
| beşyüzlü |
840.048 |
0 |
| dörtyüzlü |
27.312 |
0 |
| çok yüzlü |
0 |
439.562 |
| Toplam Hücre |
1.177.828 |
761.976 |
Çizelge.1) Yukarıda tanımlana betik üzerinden elde edilen üçgen temelli örgü ile polyDualMesh ile çokgene dönüştürülmüş örgüler arasındaki fizikî karşılaştırma.
>> Önceki Bölüm: Gmsh ile Eksensimetrik Düzenli Örgü İmâli
♦ Kaynaklar1. Gmsh genelağ sitesi - http://gmsh.info
2. An introduction to Geometrical Modelling and Mesh Generation - The Gmsh Companion, Christophe Geuzaine - Emilie Marchandise - Jean-François Remacle
|



