1953 senesinde yayınlanan, Parkin ve Kermeen tarafından gerçekleştirilmiş denel hidrodinamik çalışmalara ait, kürevî kafalar üzerinde yapılan değerlendirme [1] ile birlikte, akışuyumlu ve pürüzsüz gövdeler üzerindeki kavitasyon başlangıcının sınır tabaka ile olan etkileşimi hakkında ilk önemli adım atılmış oldu.

1963'te İsveçli iki hidrodinamikçi H. Lindgren ve C. A. Johnsson, yeni nesil torpillerin ihtiyaç duyduğu müstevî dizin sonar yerleşimlerine de uygun olacak düzlem bir burun yapısını gövdeyle çeyrek elips kullanarak birleştirme yoluyla elde edilen "değiştirilmiş eliptik" bir kafa geometrisi oluşturarak bunun hidrodinamik deneylerde kullanılmasını önerdi.[2]

Bu öneri ITTC¹ katılımcıları tarafından da kabûl gördü ve dünyanın önde gelen bütün denel hidrodinamik tesislerinde bu kafa geometrisi üzerinde kavitasyon çalışmaları yapılmaya başlandı. İki sene sonra, elde edilen ilk sonuçlar karşılaştırmalı olarak derlenerek yine Lindgren ve Johnsson tarafından sunuldu.[3]

Sonraki dönemde de uzun yıllar boyunca bu kafa geometrisi üzerindeki hidrodinamik araştırmaları devam etti. İlk zamanlar İsveçli Kafası olarak adlandırılsa da daha sonraki dönemde "Standart ITTC Kafası" tanımlaması daha yaygın olarak kullanılır oldu.

Resim.1 ve 2) Yazıya konu olan İsveçli (ITTC) kafa modelinin bir kavitasyon tüneli içinde uzak ve yakın iki görüntüsü. Alttaki resimde, oluşan kavitasyon daha rahat görülebiliyor.

O döneme kadar dünya üzerindeki pek çok hidrodinamik araştırma tesisinde çok farklı biçimlerdeki eksensimetrik kafalar üzerinde kavitaston çalışmaları yapılmakta iken, bütün bu çalışmaların tek bir kafa üzerinde yoğunlaşmasının sağlanmasıyla birlikte konu üzerinde daha önemli teknik gelişmelerin daha kısa sürede elde edilebilmesi mümkün hâle geldi.

Tek bir kafa formu üzerinde dünya çapında gerçekleştirilmeye başlayan bu çalışmalar ile de sınır tabaka davranışının kavitasyon başlangıcı üzerindeki etkilerinin fizikî kökenlerinin daha iyi anlaşılabilmesi mümkün oldu.

Mesela laminer sınır tabaka ayrılması ile laminer ayrılmaya engel olan doğal sınır tabaka geçişi durumları arasında kavitasyon davranışları belirgin farklılıklar göstermekteydi. Bilhassa Arakeri ve Acosta tarafından yayınlanan çalışmalar bu alana ışık tuttu.

Resim.3) Farklı ülkelerdeki hidrodinamik laboratuvarlarında eşdeğer Reynolds ve kavitasyon sayıları için İsveçli (ITTC) kafası üzerinde elde edilen kavitasyon oluşumlarına ait görüntüler. Açıkça görülebildiği gibi sonuçlar arasında çok büyük farklar mevcut.

Söz konusu çalışmalarda laminer ayrılmanın ortadan kalktığı sınırı belirlemek amacıyla kritik Reynolds sayısı {Re_D-krit} tanımlandı ki burada Reynolds ifadesi çap temellidir. Re_D-krit'in üstündeki değerler için kavitasyon başlangıcı genellikle laminer-türbülans geçiş bölgesinde gerçekleşir fakat suyun kimyevî ve fizikî niteliklerine ait diğer bazı değişkenlerin de durum üzerinde etkileri mevcuttur.

Bu sınırın (Re_D-krit) altında ise kavitasyonun; laminer ayrılmanın kayma katmanında veya laminer tekrar birleşme bölgesinde oluşması beklenebilir. Her iki durum için de kavitasyon başlangıcı; gerek laminer ayrılma gerekse doğal geçiş bölgesinde meydana gelen çok yüksek basınç dalgalanmalarıyla doğrudan ilişkilidir.

Çizelge.1) Bazıları [Resim.3]'de gösterilen çalışmaların da gerçekleştirildiği muhtelif Kavitasyon Tünelleri için beyan edilen Türbülans Seviyeleri (Tu), 1970'ler.

Sınır tabakanın doğal geçiş davranışı, serbest akış içindeki türbülans seviyesinin büyüklüğüne (Tu) ve cismin yüzey niteliklerine karşı son derece hassas olduğuna göre, bu iki değişkenin mesela burada bahsi geçen deney çalışmalarında elde edilen sonuçlar üzerinde de büyük bir etkisi olacağı aşikârdır.

Hemen yukarıdaki [Çizelge.1] üzerinde, çeşitli kavitasyon tünelleri için beyan edilen serbest türbülans seviyelerinin ne kadar büyük farklar gösterebildiği anlaşılabilir. İşte tam olarak bu sebeple [Resim.3] üzerinde sunulan sonuçlar üzerinde çok büyük farklılıklar ortaya çıkmıştır. Konu teknik açıdan, her şeyin kontrol altında olduğu deney ortamlarında bile böylesine zorlu iken, bir de gerçek şartları düşünün.

Resim.4) OpenFOAM için GMSH ile oluşturulan 2B Eksensimetrik düzenli çözüm örgüsü. Kafa üzerindeki her noktada
yArtı < 0,5.

gamma-Re_θ,t

Tâkip edecek hesaplamalı çalışmalar için de bu duruma uygun bir sayısal yaklaşım kullanma ihtiyacı kaçınılmazdı. Bu sebeple ITTC kafası gibi bir yapı üzerinde kavitasyon çalışması yapabilmek için eldeki imkânlarla uyumlu bir yaklaşım tercih etmek gerekliydi.

Böyle bir modeli, gerçek Reynolds sayılarında, 3B ve çoksafhalı olarak DNS² veya hatta belki LES³ ile bile çözebilecek güçte bir bilgisayar ne bende ;) ne de Türkiye Cumhuriyeti toprakları üzerinde herhangi bir yerde mevcut değildi.

Mecburen 2B olarak ve ancak RANS⁴ yaklaşımı ile problem üzerinde kısıtlı ölçüde çalışma yapabilmek mümkün olacaktı. Bu sebeple konunun OpenFOAM kullanılmak suretiyle ve Gmsh ile oluşturulacak bir 2 Boyutlu eksensimetrik ITTC (İsveçli) kafa modeli [Resim.4] için ele alınmasına karar verildi.

İkinci önemli tercih kullanılacak türbülans modelinin seçimiydi. Yukarıdaki ilk bölümde denel çalışmalar temelinde açıklandığı üzere sınır tabaka davranışının kavitasyon başlangıcı üzerindeki büyük etkisi kısaca ifade edilmeye çalışılmıştı ki bu durumda bir geçiş modeli kullanma ihtiyacı kaçınılmazdı. Böyle bir çalışmayı tam türbülanslı herhangi bir sıradan türbülans modeli ile yapmaya çalışmak tamamen mantıksız bir hareket olacaktı.

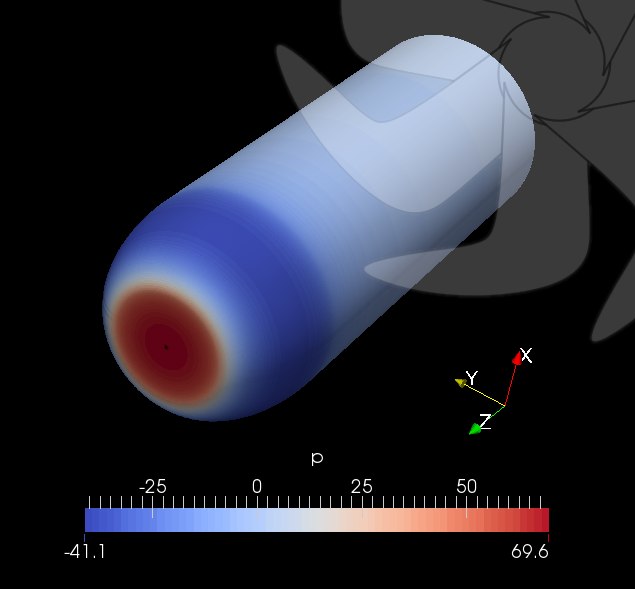
Resim.5) ITTC (İsveçli) Kafası üzerinde OpenFOAM ile hesaplanan basınç dağılımı.

RANS için kullanılabilecek geçiş modellerini iki temel gruba ayırmak mümkün olabilir ki her ikisi de daha önce bazı örneklerle kısaca ele alınmıştı:

1. İlki k-kL-omega gibi laminer kinetik enerjinin modellenmesine dayanan yaklaşımlardır. Bu tür yöntemler bazen iyi sonuçlar verebilse de aynı etkinliği her şart altında üretemedikleri için kullanılmalarında bazı güçlükler mevcuttur, üzerinde çalışılan k-v2-omega gibi daha yeni uyarlamalar ile bu hususta bazı iyileşmeler elde edilmesi muhtemel olmakla birlikte bu çalışmada söz konusu yöntemlerin kullanıldığı bir yaklaşım tercih edilmedi.
2. İkincisi denel doğrulamalarla elde edilen verilerin yerel değişkenler halinde HAD nakil denklemleriyle tümlenmesi kavramına dayanan LCTM⁵ sınıfından yaklaşımlardır. k-ωSST temelli bu tür bir model ile yapılan denemeler daha önce E387 kanat kesiti üzerinde gösterilmişti ki elde edilen sonuçlar mükemmel olarak nitelendirilebilirdi.

Şimdi yine LCTM kökenli bir yaklaşım ama bu sefer Spalart-Allmaras temelli olarak geliştirilmiş bir başka geçiş modeli kullanılacak: SA-gammaRe_θ,t [9]

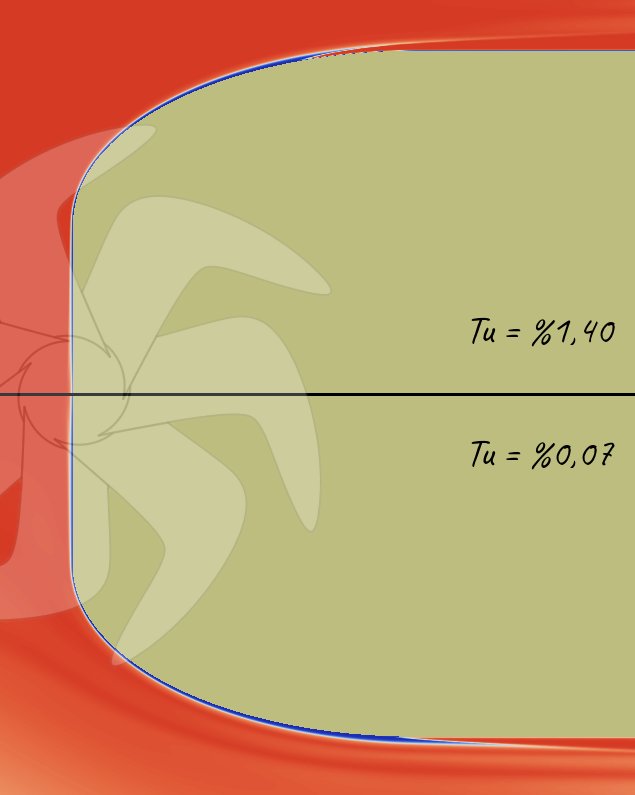
Resim.6) ITTC (İsveçli) Kafası üzerinde OpenFOAM kullanılarak ve SA-gammaRe_theta,t türbülans modeli ile hesaplanan sınır tabaka üzerindeki laminer-türbülans geçiş davranışı. İki farklı ve aşırı uçlarda sayılabilecek türbülans yoğunluğu seviyesinin geçiş bölgesi üzerindeki etkisi açıkça görülebiliyor.
[Çizelge.1] üzerinde görülebileceği üzere sıradışı olmayan bir kavitasyon tüneli için gerçekçi türbülans yoğunluğu burada sunulan iki değerin ortalaması civarındadır.

Tabii Spalart-Allmaras temelli geçiş modeli tercihinin başka bazı mâkûl sebepleri de var, daha hızlı olması, daha kolay yakınsaması, ihtiyaç halinde çalışmaya DES⁶ ile devam edebilmenin çok daha rahat olması vesaire gibi. Fakat SA ile kavitasyon benzetiminde yeterli hassasiyet elde edilemezse k-omega temelli bir geçiş modeli ile devam etmek de gerekebilir.

İlk safhada, henüz kavitasyon modellemesine geçmeden önce SA-gammaRe_θ,t modelinin yeteneklerini ve ITTC kafası üzerindeki geçiş davranışını nasıl çözebildiğini incelemek gerekliydi. [Resim.6] üzerinde sonuçlardan bir numune gösterildiği üzere elde edilen laminer-türbülans geçiş çözümleri yayınlanmış deney sonuçlarıyla mükemmel bir örtüşme sağladı. Böylece ikinci aşamada bu modeli ilk çoksafhalı kavitasyon denemelerinde kullanmanın da önü açılmış oldu...

Türkiyenin Torpilleri

Tabii bir de meselenin ister istemez geldiği bu yön var. Şu anda ülkede en az üç adet torpil çalışması yürütülüyor; Akya, Tork ve Orka. Buna mukâbil Cumhuriyet tarihi boyunca bugüne kadar bu alanda yapılmış nazarî ve tecrübî gerçek ar-ge çalışması miktarı tam olarak "Sıfır!". Muhtemelen yine pek yakında duyacağımız gibi bu çalışmaların sonuçları da her zaman olduğu gibi hem %100 milli hem de dünyanın en iyileri olarak tescillenecek. Bu da bize has özel bir yetenek olsa gerek...