Basınç taşımak amacıyla tasarlanan ince cidarlı kubbeler için kullanılan geometrik şekillerden birini de melez küre olarak da tanımlanabilecek cisimler meydana getirir. Şimdi burada simitkürevî olarak adlandırılacak olan yapılardan kısaca bahsedilecektir.

Simitküre ifâdesi adından da anlaşılabileceği üzere daire kesitli bir simit ile bir (sığ) kürenin teğet hattında birleştirilmesiyle elde edilen kubbe yapısını tanımlamaktadır ki cismin genel yapısı aşağıdaki [Resim.2] üzerinde görülebilir.

Simitkürevî kabukların basınç altındaki kararlılıklarının analitik ve denel olarak incelenmesi yönünde uzun yıllardır çalışılmaktadır. Bilinen en meşhur denel faaliyetler İngiltere'de Liverpool Üniversitesinde 1980'lerde gerçekleştirilmiştir ki esas itibarı ile denizaltı inşa teknolojisine dönük bir arge çalışması olarak da değerlendirilebilir.

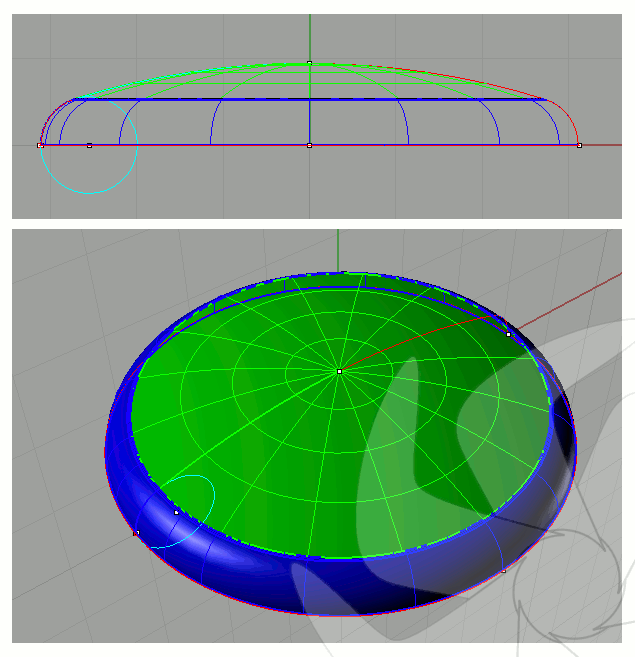
Resim.1) Buradaki hesaplamalı çalışmalar için kullanılan simit-küre geometrileri için hazırlanan 3B yüzey modellerinden biri.
Mavi bölge simit, yeşil bölge ise (sığ) küre temelli iki kabuktur ve her iki cisim teğet hattı boyunca birleştirilmiştir.

İnceleme için, kubbe yüksekliği değişkenine bağlı olarak dört adet farklı simitküre modeli oluşturuldu. Daha önceki burkulma çalışmalarına paralel olarak yine 6,2m (2R) çapındaki bir silindire bağlanmak üzere kabuk eleman temelli hesaplama örgüleri ise Gmsh [1] ile elde edildi.

Silindir (kubbe tabanı) yarıçapına (R) bağlı olarak yükseklikler için 0,15R - 0,30R - 0,45R ve 0,60R olarak belirlendi. Bu kez yüzey modelleri doğrudan Gmsh yerine Rhinoceros3D ile imâl edildi ve *.stp olarak ihraç edilerek örgü oluşturulmasında kullanıldı.

 ♦ gmsh:
// simitKüre temelli bir kubbe modeli
// yüzey modeli rhino3d'den .stp (203) olarak geldi;
// http://uskudar.biz/dosyalar/030x4.stp.tar.gz
 
// *iges ve *.stp ithâl edebilmek için geometri çekirdeğinin başlatılması
SetFactory("OpenCASCADE");  
 
// İthâl modeller üzerindeki yüzey parçalarının birleştirilebilmesi için
// farklı şartlarda "geometry.tolerance" değerinin değiştirilmesi gerekebilir
Geometry.Tolerance = 0.0001;
Geometry.OCCSewFaces = 1;
 
Merge "030x4.stp";    // 3B modelin ithâl edilmesi
 
// modelin ölçeklendirilmesi
// burada mm, metreye çevriliyor
Dilate {{0, 0, 0}, 0.001}
  { Surface{1,2,3,4};
}
 
// eğrilerin düğüm sayılarının ayarlanması
Transfinite Line {9,11,15,13} = 51;
Transfinite Line {10,12,14,16} = 61;
 
// üçgen temelli örgülerin serbest dörtgene dönüştürülmesi için
Recombine Surface "*";
 
// CalculiX'e özel bâzı ayarlamalar
Mesh.SecondOrderIncomplete=1;    // ikinci derece eleman üretildiğinde gerekeli
Mesh.SaveGroupsOfNodes = 1;      // düğüm gruplarının kaydedilmesi için
Mesh.ElementOrder = 2;           // ikinci derece elemanlar
 
// adlandırmalar
Physical Line("mesnet") = {10,12,14,16}; 
Physical Surface("kafa") = {1,2,3,4};

Böylece Gmsh'ye yeni başlayanlar veya başlayacak olanlar, herhangi bir yazılım ile meydana getirilmiş 3B (veya 2B) bir yüzey modelinin veya katı modelin örgü oluşturmakta nasıl kullanılabileceği hakkında kolayca fikir sahibi de olabilecekti ki yukarıdaki numune betik ile anlaşılabileceği gibi bütün işlem sâdece birkaç satırdan ibârettir.

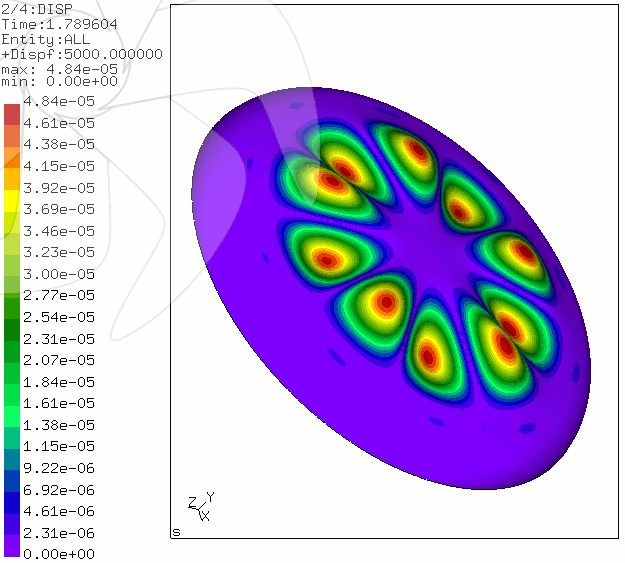
Resim.2) simitKüre geometirlerinden biri için Calculix CCX ile burkulma (ilk mod) sonucu.

Buradaki sonuçlar için kullanılan 3B yüzey modellerinden biri (0,30R) şu bağlantıdan *.stp olarak indirilebilir. İkinci safhada da hemen yukarıdaki *.geo dosyası ile birlikte kullanılarak hesaplama örgüsü kolayca imâl edilip, CalculiX (veya ihtiyaca göre farklı bir çözücü) için ihrac edilebilir.

Söz konusu dört simitküre geometrisi için doğrusal burkulma yaklaşımıyla ve yine 25mm HY80 için çözümler elde edilmiştir ve ayrıntılar [Çizelge.1] üzerinde görülebilir.

Kürevî Kubbelerin Karşılaştırılması

Daha önce ele alınan yarıküre, eliptik küreler ve sığ küreler ile birlikte buradaki simitküre geometrilerine ait ilk sonuçların ortaya çıkmasıyla, aday kubbe seçenekleri hakkında hızlı bir karşılaştırma artık yapılabilir hâle geldi.

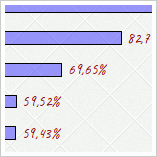
Çizelge.1) Kürevi kubbe seçeneklerinin temel hatlarıyla karşılaştırılması.

İnce cidarlı kürevî kabukların burkulması hakkındaki bu dört çalışmanın özeti [Çizelge.1] ve [Resim.3] üzerinde görüldüğü gibidir, üzerinde çok fazla yorum yapmaya şimdilik pek ihtiyaç yok.

Bu dağılımlar bazı fikirler verebilmekteyse de gerek daha önce kısmen bahsi geçen yapısal kusurların incelenmesi ve gerekse doğrusal olmayan etkilerin ele alınması ihtiyacı mevcuttur...

Resim.3) İncelenen bütün kürevî kubbeler için doğrusal yaklaşımla elde edilen burkulma yüklerinin en iyi yük taşıyıcı şekil olan yarıküre ile oran temelinde karşılaştırılması.

Dolayısıyla konunun ilerleyen safhalarında torpil kovanları gibi donanımlar için gereken kubbe nüfûziyetlerinin burkulma davranışları üzerindeki etkileri, doğrusal olmayan burkulma davranışlarının karşılaştırılması ve belki sualtı infilâkı ile oluşan etkilere karşı muhtelif kubbe seçeneklerinin dinamik tepkilerinin incelenmesi söz konusu olabilir...